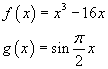
Funzioni
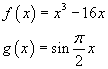
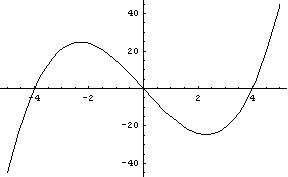
Il grafico della funzione f è una cubica, definita su tutto R; è dispari, quindi simmetrica rispetto all'origine, passa per l'origine dove ha un flesso. f è positiva per
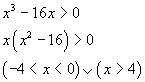
È negativa per
![]()
Ha zeri {-4; 0; +4}
Per x→∞ f diverge positivamente, per x→-∞ diverge negativamente. Una cubica non ammette asintoti.
f è crescente dove la derivata prima è positiva:
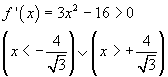
È decrescente per
![]()
f ha un massimo
![]()
e un minimo simmetrico
![]()
La derivata seconda
![]()
è una funzione dispari, negativa per x negative, positiva per x positive, nulla per x nullo. La concavità ne segue l'andamento. Come previsto c'è un flesso obliquo nell'origine.
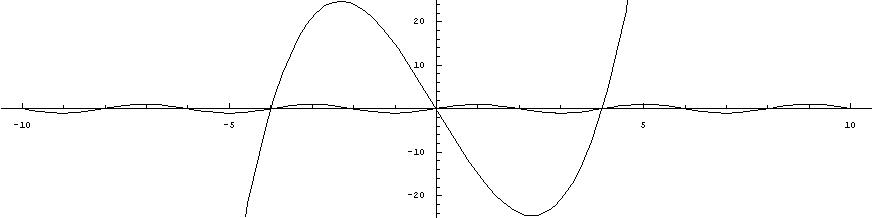
La funzione g è una sinusoide di periodo uguale a 4. Assumendo come ben noto l'andamento delle sinusoidi non si ritiene necessario proporne lo studio dettagliato.Il grafico presenta punti stazionari ('a tangente orizzontale') ogni quarto di periodo con l'alternanza di massimi e di minimi di valore rispettivamente +1 e -1, a partire dal primo massimo di ascissa positiva (1;1) seguito dal minimo (3;-1) e successivamente (5;1), (7;-1), (9;1). Con ascisse negative (-1;-1), (-3;1), (-5;-1), (-7;1), (-9;-1).
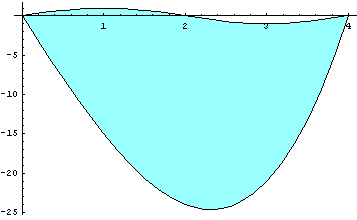
L'area della figura è data dall'integrale
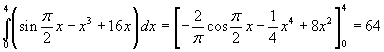
Le rette indicate intersecano solo la cubica. Le intersezioni richieste si ottengo risolvendo i seguenti sistemi:
![]()
![]()
L'equazione risolvente del primo sistema è
![]()
È immediato notare che una soluzione è 1. Dividendo il polinomio per x-1 e uguagliando a 0 il quoziente si ottiene
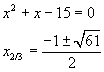
Ovviamente la soluzione pertinente è quella positiva. Quindi le prime due ascisse richieste sono
![]()
L'equazione risolvente del secondo sistema è
![]()
Per approssimare le soluzioni di questa equazione conviene l'uso del metodo delle tangenti: data una stima iniziale x0, la successione
![]()
fornisce sempre migliori approssimazioni. Si ottiene
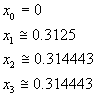
e inoltre
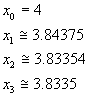
Il volume richiesto può essere pensato come somma di parallepipedi infinitesimali per i quali l'area di base è
![]()
e l'altezza è dx. Si ha quindi
![]()
L'integrale nel minuendo è già stato calcolato: il minuendo vale 320. Per il calcolo del sottraendo si ha, integrando per parti
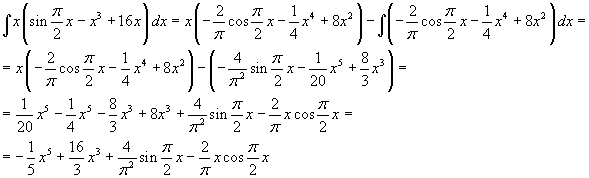
Quindi
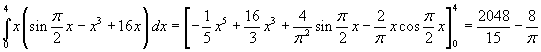
In definitiva si ottiene
![]()
186m3 sono 186000 litri.