Una geometria, cioè un sistema assiomatico-deduttivo basato su un insieme di postulati e di regole di deduzione non contraddittorie, non ha in sè nessun valore ontologico, cioè non può dirci nulla sulla natura della realtà fisica.
Le teorie fisiche, allo scopo di fornire la descrizione di ben definite classi di fenomeni (non la 'realta', ma ciò che possiamo osservare), rappresentano diverse grandezze come elementi di spazi vettoriali normati. In alcuni casi, come nella meccanica classica newtoniana, risulta adeguato l'uso della metrica euclidea; in altri casi, come nella teoria della Relatività Generale, risulta indispensabile l'adozione di metriche non euclidee.
Il quadrato della distanza di un punto Q della curva proposta dal punto indicato risulta
![]()
con x ≥ 0. Il grafico di tale funzione è rappresentato da un arco di parabola che ha il suo minimo nel vertice. Dunque
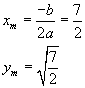
La distanza minima risulta
![]()
Il problema si risolve molto velocemente applicando il teorema di Guldino: il volume di rotazione è dato dal prodotto dell'area della superficie ruotata per la lunghezza della circonferenza percorsa dal suo baricentro. La superficie ruotata è quella compresa tra la sinusoide e l'asse delle ascisse. È immediato dimostrare che la sua area è 2. Data la simmetria della superficie, il suo baricentro dista π/2 dall'asse di rotazione, dunque
![]()
Si tratta di risolvere l'equazione
![]()
Sviluppando i coefficienti binomiali si ottiene
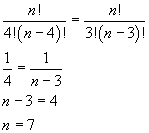
Più velocemente si può osservare che i coefficienti binomiali sono uguali se e solo se sono simmetrici e i termini dell'equazione sono simmetrici solo se n è uguale a 7.
L'affermazione di Salviati, letta nel contesto, si rivela una maliziosa domanda trabocchetto per Simplicio, l'interlocutore aristotelico. Salviati, che nel dialogo propone le tesi galileiane, sa bene che non è vero. Dato che ad ogni numero naturale corrisponde un quadrato e viceversa, l'insieme dei naturali e l'insieme dei loro quadrati sono equipotenti, cioè hanno la stessa cardinalità.
Detta α la metà dell'angolo di apertura del cono (0≤α≤π/2), per il teorema della corda, il raggio di base r del cono è
![]()
e l'apotema
![]()
La superficie laterale s(α) risulta
![]()
La derivata prima è
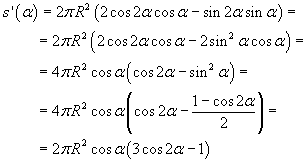
La derivata prima è positiva per
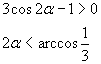
s(α) ha un massimo per
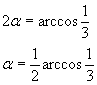
Si ha
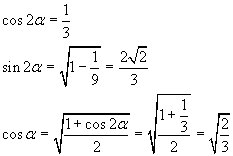
La superficie massima risulta
![]()
Con la misura del raggio assegnata si ha
![]()
In ogni singolo quesito la probabilità p successo è 1/4; la probabilità q di insuccesso è 3/4. Per il teorema delle prove ripetute si ha che la probabilità che nessuna risposta sia corretta è
![]()
La probabilità che solo una risposta sia corretta è
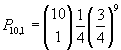
La probabilità che almeno due risposte siano corrette è la probabilità complementare alla somma di queste due:
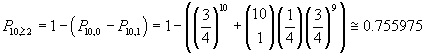
Questo quesito, ormai abituale nelle prove di maturità, fa riferimento ad uno dei problemi classici della antica geometria greca; gli altri sono la duplicazione del cubo e la trisezione dell'angolo.
Per gli antichi geometri greci nella soluzione di un problema erano ammesse solo costruzioni con riga e compasso e, nonostante numerosi tentativi, era risultato impossibile con tale metodo, dato il diametro, costruire un segmento di lunghezza pari alla circonferenza: questo è il significato della locuzione quadratura del cerchio.
Nel linguaggio moderno, ciò equivale ad affermare che il numero π, cioè il rapporto tra circonferenza e diametro, è un reale trascendente, cioè non esprimibile con radicali.
L'espressione quadratura del cerchio è passata nel linguaggio ordinario come metafora per soluzione di un problema complicatissimo.
Dette a e b le misure dei cateti del triangolo, si assuma come origine O del sistema di riferimento cartesiano il vertice dell'angolo retto, come assi x e y le rette dei cateti e come asse la retta per O perpendicolare al piano xy. Sia A il punto (a;0) e B il punto (0;b). Detto P(x,y,z) un punto dello spazio si ha
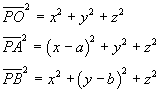
L'uguaglianza delle distanze implica
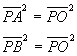
cioè
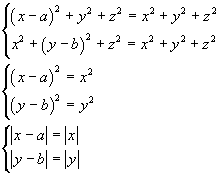
L'unica soluzione accettabile è
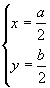
Il luogo richiesto è l'insieme dei punti dello spazio che hanno queste coordinate x e y, qualunque sia la loro coordinata z, cioè la retta perpendicolare al piano del triangolo per il punto medio dell'ipotenusa.
La risposta corretta è la D. La curva I è una cubica simmetrica rispetto all'origine, quindi dispari, e con un unico zero reale, di equazione
![]()
Il suo integrale indefinito è rappresentato dalla curva II
![]()
funzione pari con intersezione con l'asse y di ordinata negativa e due zeri reali. Infine l'integrale di quest'ultima è
![]()
funzione dispari con tre zeri reali.