(a cura di Roberto Bigoni)
Si denominano integrali binomiali gli integrali di forma
![]()
La denominazione è giustificata dal fatto che la funzione integranda è la potenza di un binomio che, per valori naturali di n, può essere agevolmente sviluppata in
![]()
Integrando questo sviluppo da 0 a 1 si ottiene facilmente
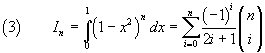
Calcolando i primi termini di questa successione si ha
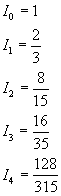
Si osserva che
![]()
Viene quindi spontaneo congetturare che, in generale, per ogni n naturale maggiore di 0,
![]()
![]()
In particolare
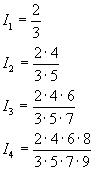
In generale
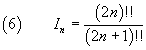
Nella (6) il doppio punto esclamativo rappresenta il doppio fattoriale (o semifattoriale) del numero che lo precede. Come si vede dagli esempi, se un numero è pari, il suo doppio fattoriale è il prodotto del numero stesso per tutti i pari che lo precedono; analogamente, se il numero è dispari, il suo doppio fattoriale è il prodotto del numero stesso per tutti i dispari che lo precedono.
Nella pagina sull'induzione matematica di questo sito si propone una dimostrazione della (6) osservando che In può essere espresso anche nel seguente modo
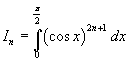
In conclusione, per ogni numero naturale n si ha
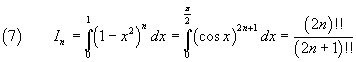
ultima revisione: Maggio 2018