(a cura di Roberto Bigoni)
L'ellisse ε di semiassi a e b (a > 0; b > 0; a ≥ b) in un sistema cartesiano ortogonale Oxy con origine O nel suo centro di simmetria e assi cartesiani sovrapposti ai suoi assi, ha equazione
![]()
L'equazione dell'arco di ε contenuto nel primo quadrante è
![]()
quindi
![]()
![]()
![]()
La lunghezza dl di un tratto infinitesimale di arco è data da
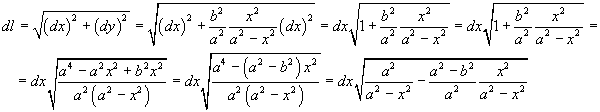
Osservando che
![]()
dove e è l'eccentricità di ε, si ottiene
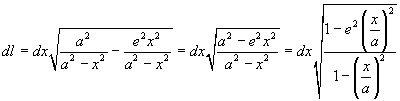
La lunghezza q dell'arco è data dall'integrale
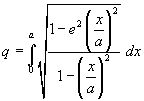
Introducendo la variabile t
![]()
si ottiene infine
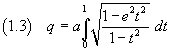
In definitiva la lunghezza dell'ellisse è espressa da
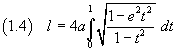
L'integrale a secondo membro della (1.3) è detto integrale ellittico completo di seconda specie:
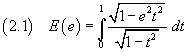
Con un ulteriore cambiamento di variabile se ne può semplificare l'espressione. Infatti ponendo
![]() si ottiene
si ottiene
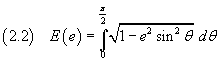
La funzione integranda può essere sviluppata come potenza di un binomio
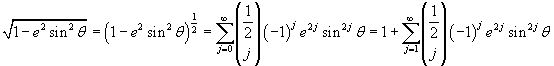
dunque
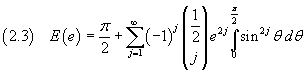
Osservando che, per j ≥ 1,
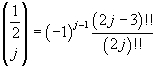
dove il doppio punto esclamativo rappresenta il doppio fattoriale dell'intero cui si riferisce, si ottiene
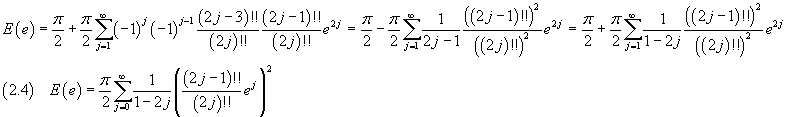
Dalle (1.4) e (2.4) per la lunghezza dell'ellisse di semiasse maggiore a e eccentricità e si ottiene
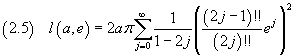
In modo analogo si può ottenere lo sviluppo in serie dell'integrale
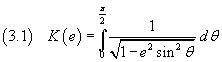
detto integrale ellittico completo di prima specie.
Sviluppando in serie binomiale la funzione integranda si ha
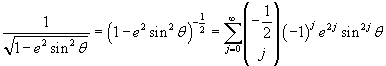
Risulta quindi
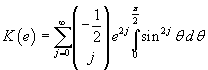
Dato che
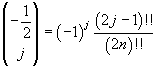
si ottiene
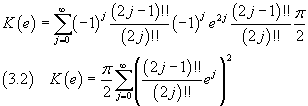
Usando le trasformazioni di Landen si dimostra che l'integrale ellittico di prima specie è esprimibile in funzione della media aritmetico-geometrica
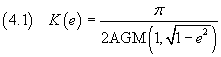
La (4.1) permette di approssimare il valore di K(e) con un algoritmo abbastanza veloce e preciso, di cui si presenta un versione Javascript che approssima anche E(e). La funzione Javascript è dedotta da una pagina di A. C. M. de Queiroz.
function ellipticInt()
{
var a, b, a1, b1, amb, E, i, k, kk, IK, IE;
k = parseFloat(document.getElementById("input_e").value);
kk = k*k;
a = 1;
b = Math.sqrt(1-kk);
E = 1-kk/2;
i = 1;
do
{
a1 = (a+b)/2;
b1 = Math.sqrt(a*b);
amb = a-b;
E -= i*amb*amb/4;
i *= 2;
a = a1;
b = b1;
} while (Math.abs(a-b)>1e-15);
IK = Math.PI/(2*a);
IE = E*IK;
document.getElementById("agm").value = a;
document.getElementById("intK").value = IK;
document.getElementById("intE").value = IE;
}
Per il calcolo di K(e) e E(e) in Mathematica (Wolfram) sono disponibili le funzioni EllipticK[m] e EllipticE[m]: va osservato che, a causa della diversa convenzione sulla notazione, l'argomento m delle funzioni di Mathematica deve essere uguale al quadrato dell'argomento e qui adottato. Provare WolframAlpha
Si dice pendolo ideale un sistema costituito da una massa puntiforme m posta ad una estremità di un'asta inestensibile di lunghezza l e massa nulla. Si assume il sistema privo di attriti.
Il sistema è situato in un campo costante di accelerazione gravitazionale di intensità g e l'asta è libera di ruotare attorno all'altra estremità fissa nel punto O. Si assume nulla l'energia potenziale gravitazionale del sistema quando la massa è situata sulla verticale per O di sotto di O.
Inizialmente l'asta è ruotata di un angolo antiorario θ0 rispetto alla verticale passante per O e tenuta ferma in tale posizione
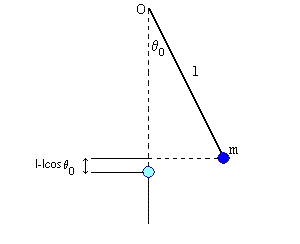
In tale stato la massa ha energia totale
![]()
All'istante t0=0 l'asta è lasciata libera. La massa inizia a cadere e θ a diminuire. Per θ0 > θ > 0 la massa ha sia energia potenziale sia energia cinetica. Per un generico angolo θ l'energia potenziale è
![]()
e la sua energia cinetica è
![]()
Dato che la massa percorre una traiettoria circolare, si ha
![]()
quindi
![]()
Per il principio di conservazione dell'energia meccanica
![]()
Semplificando
![]()
![]()
Dalla (5.1) si ottiene
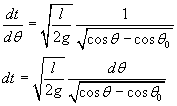
Indicando con T il periodo del pendolo, cioè la durata di un'oscillazione completa, la durata della discesa da θ0 a 0 risulta
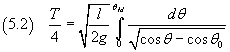
Con la sostituzione di variabile
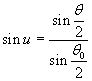
si ottiene
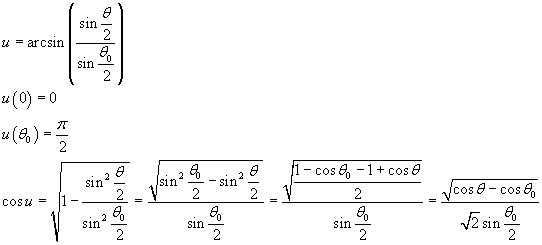
Inoltre
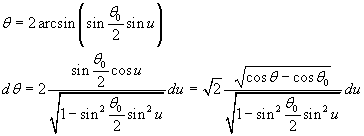
Dalla (5.2) si ottiene quindi
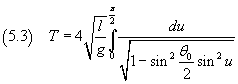
L'integrale nella (5.3) è un integrale ellittico di prima specie e per la (3.2) vale
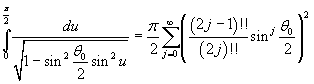
In definitiva
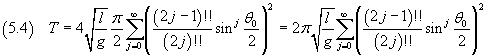
Se θ0 è molto piccolo, le potenze pari del seno della sua metà diventano trascurabili (sperimentalmente al di sotto della sensibilità degli strumenti) e la (5.4) si riduce a
![]()
ultima revisione: Maggio 2018