(a cura di Roberto Bigoni)
1. ![]()
Le funzioni a numeratore e a denominatore della frazione sono entrambe continue su tutto ℜ ma entrambe si annullano per x=0. È dunque impossibile calcolare immediatamente il limite della frazione come rapporto tra i limiti del numeratore e del denominatore.
In un intorno di 0 numeratore e denominatore soddisfano ai requisiti del teorema di De L'Hôpital e quindi il limite della frazione può essere calcolato come rapporto tra i limiti delle derivate per x→0, ottenendo immediatamente il valore 1.
Il calcolo del limite è ancora più diretto se si utilizza lo sviluppo in serie dell'esponenziale naturale
![]()
È anche possibile dedurre il valore del limite applicando il teorema del confronto.
Si considerino le funzioni
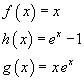
Graficandole insieme in un intorno di 0 si ha
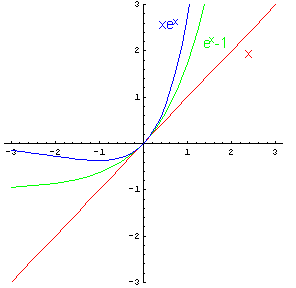
Il grafico evidenzia che per x non nulle
![]()
Ovviamente un grafico, pur essendo indicativo, non può avere valore di prova matematica, ma non è difficile verificare separatamente la validità di tutte le disequazioni. Per ogni x positivo si ha quindi
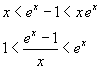
Poiché per x→0 le funzioni esterne tendono a 1, anche la funzione compresa tra di esse tende a 1.
Se x è negativo, dividendo le tre funzioni per x i confronti cambiano di verso e la situazione non cambia.
Volendo evidenziare geometricamente i confronti tra le tre funzioni nell'intervallo ]0 ; 1[, si può procedere nel seguente modo.
Si graficano le tre funzioni
![]()
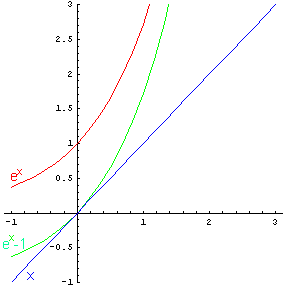
Si traccia la retta dei punti di ascissa x ∈ ]0;1[ che interseca le tre curve e si costruiscono i rettangoli come in figura. Le lettere sovrapposte ai rettangoli ne rappresentano le rispettive misure.
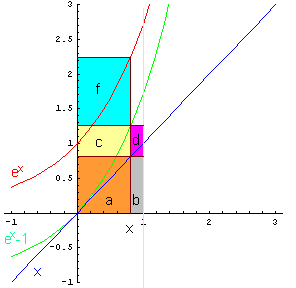
a+b = x;
a+b+c+d = ex-1; dunque ex-1 > x;
f+c+a = x ex
f = x; quindi x ex > x;
x ex - (ex - 1) = a - d
Da a > d segue che x ex > ex - 1
2. ![]()
Se nel limite (1) si pone
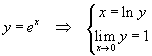
si ottiene
![]()
In generale
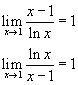
3. ![]()
Se nel limite (2) si pone
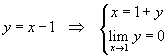
si ottiene
![]()
In generale
![]()
Applicando una nota proprietà dei logaritmi si ha
![]()
Ammettendo che il limite di un logaritmo sia uguale al logaritmo del limite si ottiene
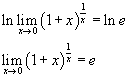
4. 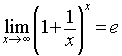
Se nel limite (3) si pone
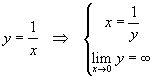
si ottiene
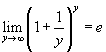
In generale
![]()
ultima revisione: 25/06/2016