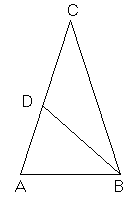
È detto triangolo aureo di primo tipo ogni triangolo isoscele in cui gli angoli alla base sono doppi dell'angolo al vertice. Poiché la somma degli angoli interni di un triangolo è π, l'angolo al vertice misura π/5 (36°) e gli angoli alla base misurano 2π/5 (72°).
La ragione dell'attributo aureo risiede nel fatto che in tali triangoli la base è la parte aurea del lato.
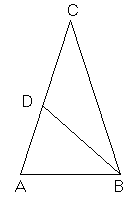
Tracciando la bisettrice dal vertice B che interseca il lato opposto in D, i triangoli ABC e ABD risultano simili. Vale quindi la proporzione
![]()
I triangoli ABD e BDC risultano pure isosceli: in particolare i tre segmenti AB, BD, DC risultano congruenti. Si ha quindi che AD = AC-AB. La base AB equivale quindi alla parte aurea del lato AC.
I triangoli simili al triangolo BCD, cioè i triangoli isosceli in cui l'angolo al vertice è triplo degli angoli alla base, sono detti triangoli aurei di secondo tipo. In questi triangoli isosceli il lato è la parte aurea della base.
Una immediata conseguenza della proprietà dei triangoli aurei
di primo tipo è che
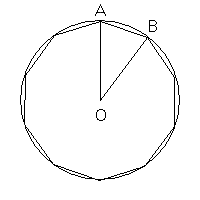
il lato del decagono regolare inscritto in una circonferenza è
la parte aurea del raggio.
Un decagono regolare può essere scomposto in dieci triangoli aurei aventi le basi sui lati e vertici in comune. I lati uguali dei triangoli coincidono con raggi della circonferenza circoscritta.
La misura del lato del decagono risulta
![]()
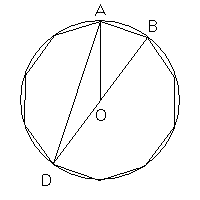
Prolungando il raggio BO fino al punto D diametralmente opposto e tracciando il segmento DA si ottiene il triangolo rettangolo BAD che ha come ipotenusa il diametro BD e in cui l'angolo acuto in D misura π/10 (18°); si può quindi dedurre il valore del seno di π/10 (18°)
![]()
Dal seno è poi immediato dedurre il coseno.
![]()
La misura del segmento AD risulta
![]()
Indicando con C il punto medio del minore degli archi AD, il triangolo ACD risulta un triangolo aureo di secondo tipo. I segmenti AC e CD sono lati del pentagono regolare inscritto. Il segmento AD è una diagonale di tale pentagono. Dunque il lato del pentagono regolare inscritto in una circonferenza è la parte aurea della diagonale.
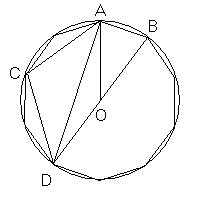
La misura del lato del pentagono risulta
![]()
Tracciando le diagonali di un pentagono regolare si ottiene il pentagono stellato, assunto a simbolo della scuola di Pitagora e caricato di significati esoterici nella tradizione ermetica, cabalistica e massonica.
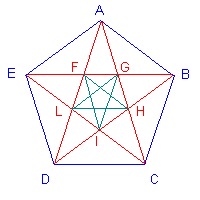
In questa figura il segmento AE è la parte aurea del segmento AD, il segmento AF è la parte aurea del segmento AE, il segmento FG è la parte aurea del segmento AF. La successione potrebbe continuare all'infinito se si tracciassero le diagonali del pentagono FGHIL, poi quelle del pentagono delimitato da queste diagonali, e così via.