English version

1. La sezione aurea di un segmento e il numero aureo

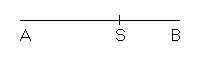
Dato un segmento AB se ne esegue la sezione aurea ('il taglio dorato') individuando un suo punto interno S tale che il quadrato di lato AS sia equivalente al rettangolo di lati AB e SB.
In modo del tutto equivalente si può dire che il segmento AS deve essere medio proporzionale tra AB e SB.

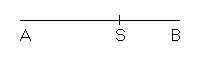
Dette λ la misura del segmento AB e σ la misura del segmento AS si ha

Risolvendo la proporzione rispetto a σ si ottiene

Il segmento AS è detto parte aurea del segmento AB.

Il rapporto tra un segmento e la sua parte aurea è detto numero aureo ed è solitamente indicato con il simbolo Φ.

Il reciproco del numero aureo Φ è indicato con il simbolo φ.

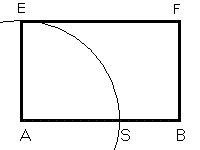
La relazione tra σ e λ suggerisce un modo per eseguire la sezione aurea di un segmento AB di lunghezza λ con riga e compasso:

• Dato AB di misura λ, si costruisce il triangolo rettangolo che ha per cateti AB e BC uguale alla metà di AB; l'ipotenusa AC ha misura
• Si traccia la circonferenza Δ di centro C e raggio CB che interseca l'ipotenusa in D.
  Il segmento AD ha misura , cioè la misura della parte aurea.
• Si traccia la circonferenza Σ di centro A e raggio AD che interseca AB in S. Il segmento AS ha misura uguale a quella di AD, quindi S è il punto che determina la sezione aurea.

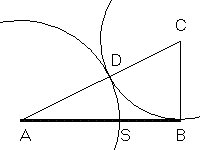
La definizione della sezione aurea implica che il segmento SB è a sua volta la parte aurea del segmento AS.

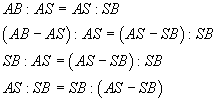
La perpendicolare al segmento AB per A interseca Σ nel punto E. Il rettangolo di lati AB e AE è detto rettangolo aureo.

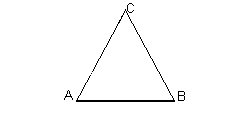
Se, viceversa, dato un segmento di misura σ, si vuole costruire un segmento di lunghezza λ di cui il precedente sia la parte aurea, si può operare nel seguente modo:

• si traccia il segmento AB di misura σ e si costruisce su di esso il triangolo equilatero ABC;

  

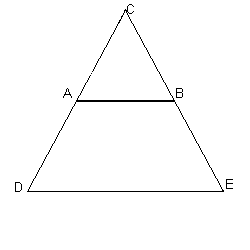
• si raddoppiano le misure dei lati CA e CB, ottenendo il triangolo equilatero DEC;

  

• si traccia la circonferenza γ circoscritta al triangolo DEC;

  

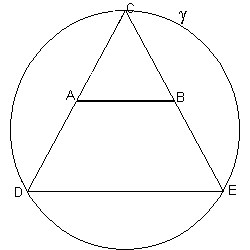
• si prolunga il segmento AB fino ad intersecare γ nei punti P e Q;

  

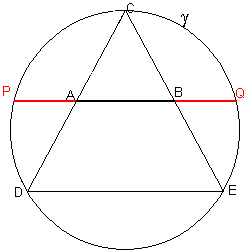
  i segmenti PB e AQ sono tali che AB è la loro parte aurea.

Infatti, per il teorema delle corde secanti

e, poiché

BQ è congruente a PA che è dato da , quindi

Lo schema di composizione fornito dal rettangolo aureo ha avuto notevole importanza nella storia dell'arte occidentale.