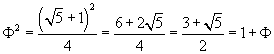
Elevando Φ al quadrato si ottiene
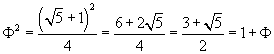
cioè
![]()
Questa relazione può essere interpretata come una definizione ricorsiva di Φ. Sostituendo alla Φ del secondo membro la definizione di Φ si ha
![]()
Queste sostituzioni possono continuare all'infinito
![]()
Viceversa, assunto come valore iniziale Φ0 qualunque valore ≥-1, aggiungendogli 1 ed estraendo la radice quadrata di questa somma, aggiungendo di nuovo 1 ed estraendo la radice della nuova somma , poi ancora aggiungendo 1 ed estraendo la radice della nuova somma e così via, si ottengono valori tanto più prossimi a Φ quante più volte si ripete il processo.
Descrivendo sinteticamente questa procedura con adatto simbolismo, si può scrivere che, dato Φ0,
![]()
Questa espressione può essere facilmente implementata in un foglio elettronico. Ad esempio, assumendo Φ0=0, si ottiene
0, 1, 1.414213562, 1.553773974, 1.598053182, 1.611847754, 1.616121207, 1.617442799, 1.617851291, 1.617977531, 1.618016542, 1.618028597, 1.618032323, 1.618033474, 1.61803383, 1.61803394, 1.618033974, 1.618033984, 1.618033987, 1.618033988, 1.618033989, 1.618033989, 1.618033989, 1.618033989, 1.618033989, ...
Dall'uguaglianza
![]()
si può ottenere anche la seguente definizione ricorsiva di Φ
![]()
Con un procedimento di sostituzioni analoghe a quelle impiegate nel caso precedente si ottiene
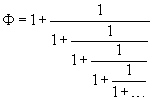
Anche in questo caso, assunto come valore iniziale Φ0 qualunque valore diverso da 0, se ne calcola il reciproco e gli si aggiunge 1; del valore così ottenuto, si calcola il reciproco e gli si aggiunge 1 e così via. Quante più volte si ripete questo procedimento, tanto più si approssima Φ.
Quindi l'espressione di Φ in frazione continua è Φ = {1,1,1,1,1,1,1,1,1,1,1,1,...}.
In notazione matematica si ha che, dato Φ0,
![]()
Se si assume come valore iniziale Φ0 un numero intero, si ottiene una successione di razionali, rappresentabili come frazioni. Ad esempio, con Φ0=1 si ha
![]()
Questa successione manifesta interessanti regolarità:
Queste proprietà della successione suggeriscono un modo alternativo di ottenere la stessa successione.
Si definisce la successione dei numeratori fi
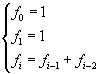
Da questa definizione si ottiene appunto la successione
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
Questa successione è nota come successione di Fibonacci.
Nella successione di Fibonacci si determinano i rapporti tra ogni numero e il precedente. Questi rapporti convergono a Φ.
![]()
La denominazione di successione di Fibonacci è dovuta al fatto che questa successione è descritta da Leonardo Fibonacci nel suo Liber Abaci del 1202, con la proposizione di un curiosa questione sulla proliferazione dei conigli.
| Liber Abaci | traduzione |
|---|---|
| Quot paria coniculorum in uno anno ex uno pario germinentur. | Quante coppie di conigli discendono in un anno da una coppia. |
| Qvidam posuit unum par cuniculorum in quodam loco, qui erat undique pariete circundatus, ut sciret, quot ex eo paria germinarentur in uno anno: cum natura eorum sit per singulum mensem aliud par germinare; et in secundo mense ab eorum natiuitate germinant. | Un tale mise una coppia di conigli in un luogo completamente circondato da un muro, per scoprire quante coppie di conigli discendessero da questa in un anno: per natura le coppie di conigli generano in un mese un'altra coppia, e cominciano a procreare a partire dal secondo mese dalla nascita. |
| Quia suprascriptum par in primo mense germinat, duplicabis ipsum, erunt paria duo in uno mense. |
Dato che la suddetta coppia si riproduce nel primo mese, bisogna raddoppiarla: nel primo mese le coppie sono quindi 2. |
| Ex quibus unum, scilicet primum, in secundo mense geminat; et sic sunt in secundo mense paria 3; | Di queste due coppie una, la prima, all'inizio del secondo mese ne genera un'altra: quindi nel secondo mese ci sono 3 coppie. |
| ex quibus in uno mense duo pregnantur; et geminantur in tercio mense paria 2 coniculorum; et sic sunt paria 5 in ipso mense; | Di queste, durante il mese, due ingravidano e all'inizio del terzo mese, generano 2 coppie di conigli: quindi, nel terzo mese, ci sono 5 coppie di conigli. |
| ex quibus in ipso pregnantur paria 3; et sunt in quarto mense paria 8; | Di queste, durante il mese, 3 ingravidano e nel quarto mese ci sono 8 coppie. |
| ex quibus paria 5 geminant alia paria 5: quibus additis cum parijs 8, faciunt paria 13 in quinto mense; | Di queste, al quinto mese, 5 coppie ne generano altre 5 che, aggiunte alle 8 coppie esistenti, fanno 13 coppie. |
| ex quibus paria 5, que geminata fuerunt in ipso mense, non concipiunt in ipso mense, sed alia 8 paria pregnantur; et sic sunt in sexto mense paria 21; | Di queste le 5 ultime nate non concepiscono durante il mese, ma le altre 8 ingravidano, quindi nel sesto mese ci sono 21 coppie. |
| cum quibus additis parijs 13, que geminantur in septimo, erunt in ipso paria 34; | Aggiungendo a queste altre 13 coppie che vengono partorite nel settimo mese, ci saranno in quel mese 34 coppie. |
| cum quibus additis parijs 21, que geminantur in octauo mense, erunt in ipso paria 55; | Aggiungendo a queste altre 21 coppie che vengono partorite nell'ottavo mese, ci saranno in quel mese 55 coppie. |
| cum quibus additis parjis [sic] 34, que geminantur in nono mense, erunt in ipso paria 89; | Aggiungendo a queste altre 34 coppie che vengono partorite nel nono mese, ci saranno in quel mese 89 coppie. |
| cum quibus additis rursum parijs 55, que geminantur in decimo mense 144; | Aggiungendo nuovamente a queste altre 55 coppie che vengono partorite, nel decimo ci saranno 144 coppie. |
| cum quibus additis rursum parijs 89, que geminantur in undecimo mense, erunt in ipso paria 233. | Aggiungendo nuovamente a queste altre 89 coppie che vengono partorite nell' undicesimo mese, ci saranno in quel mese 233 coppie. |
| Cum quibus etiam additis parijs 144, que geminantur in ultimo mense, erunt paria 377; | Aggiungendo nuovamente a queste anche 144 coppie che vengono partorite nell'ultimo mese, ci saranno 377 coppie. |
| et tot paria peperit suprascriptum par in prefato loco in capite unius anni. | Tante sono le coppie generate dalla coppia iniziale in quel luogo in capo ad un anno. |
| Potes enim uidere in hac margine, qualiter hoc operati fuimus, scilicet quod iunximus primum numerum cum secundo, uidelicet 1 cum 2; et secundum cum tercio; et tercium cum quarto; et quartum cum quinto, et sic deinceps, donec iunximus decimum cum undecimo, uidelicet 144 cum 233; et habuimus suprascriptorum cuniculorum summam, uidelicet 377; et sic posses facere per ordinem de infinitis numeris mensibus. | Si può inoltre vedere qui di fianco come abbiamo operato: abbiamo sommato il primo numero con il secondo, cioè 1 e 2; il secondo con il terzo, il terzo con il quarto, il quarto con il quinto e così via finché abbiamo sommato il decimo con l'undicesimo, cioè 144 con 233 ed abbiamo ottenuto la somma dei suddetti conigli, cioè 377 e così si può fare per un numero infinito di mesi. |
Secondo P. Odifreddi, in "Variazioni: un tema aureo" (Le Scienze, n. 436, dic. 2004), questa successione era già nota ai matematici indiani Virahanka e Gopala (1133). Molto probabilmente questi matematici, come anche Hemachandra e Pandita, continuavano una tradizione molto più antica risalente a Pingala (200 a.C.), che analizzando la metrica poetica del sanscrito, scoprì sia la regola di formazione del triangolo di Pascal (noto in Italia come triangolo di Tartaglia) sia la successione di Fibonacci.
Se infatti, partendo dal primo numero di ogni riga del triangolo, si sommano tutti i numeri in diagonale SO-NE, si ottengono i numeri di Fibonacci.
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | |
| 1 | |||||||||||
| 1 | 1 | ||||||||||
| 1 | 2 | 1 | |||||||||
| 1 | 3 | 3 | 1 | ||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||
| 1 | 5 | 10 | 10 | 5 | 1 | ||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | |||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | ||||
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | |||
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | ||
| 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 101 | 1 |
Nel software specializzato è prevista una funzione apposita per il calcolo dei numeri di Fibonacci. Ad esempio Mathematica della Wolfram ha la funzione Fibonacci[n] che può essere usata direttamente o in contesti più complessi. La figura seguente propone un esempio di calcolo dei primi 20 numeri di Fibonacci tramite Mathematica utilizzato da WolframAlpha
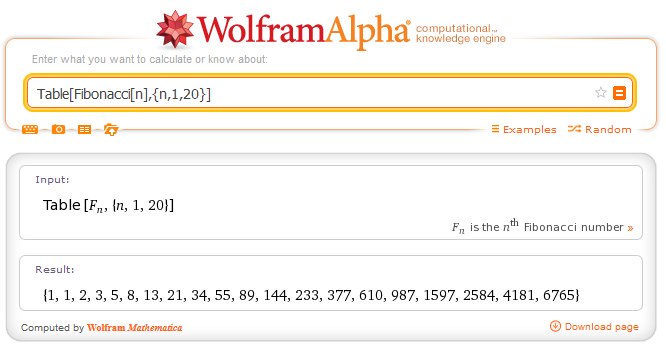
Accedendo direttamente a Wolfram Alpha si possono provare altre elaborazioni: Fibonacci con Wolfram Alpha
Dovendo provvedere una propria applicazione di una funzione generatrice dei numeri di Fibonacci, l'idea di usare un algoritmo ricorsivo, anche sul più veloce dei sistemi, risulta decisamente infelice per l'esplosione esponenziale del tempo di calcolo: per avere il termine n-simo bisogna calcolare i due precedenti; per ognuno di questi i due precedenti, quindi quattro calcoli; poi per ognuno di questi quattro i due precedenti e si va a otto, e così via.
Quindi, ad esempio, in Javascript, per quanto possa apparire formalmente elegante, non è conveniente una soluzione del tipo
function fibonacci(n)
{
if ((n==0)||(n==1)) return 1;
else return fibonacci(n-1)+fibonacci(n-2);
}
È preferibile organizzare il calcolo usando un algoritmo iterativo. Ad esempio, sempre in Javascript:
function fibonacci(n)
{
if ((n==1) || (n==2)) return 1;
else
{
var risultato, i, prec=1, precprec=1;
for (i=3; i≤n; i++)
{
risultato = precprec+prec;
precprec = prec;
prec = risultato
}
return risultato;
}
}
Questa funzione è usata nella seguente form (non usare indici maggiori di 78).
Con metodi di programmazione più evoluti, ad esempio creando in Javascript un oggetto in grado di rappresentare ed elaborare numeri naturali comunque grandi, si possono calcolare esattamente i numeri di Fibonacci senza limiti di rappresentabilità (ma il tempo di calcolo può diventare proibitivo). Ad esempio, con Javascript si possono redigere applicazioni come la seguente.
È però possibile calcolare direttamente l'ennesimo numero di Fibonacci da una combinazione lineare delle potenze ennesime di di Φ e -φ. Infatti, se si pone
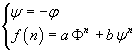
con le condizioni
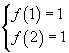
si ottiene il sistema
![]()
cioè
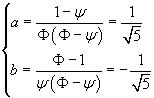
In definitiva
![]()
La funzione f(n), attribuita a J. Binet ma già nota a A. De Moivre e a L. Euler, per n naturali, calcola direttamente i numeri di Fibonacci. Infatti
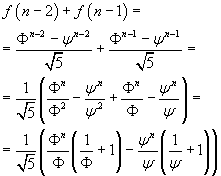
Ma dato che
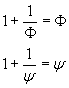
in definitiva si ottiene
![]()
Usando la funzione di Binet, il calcolo dei numeri di Fibonacci può essere impostato, in Javascript, nel seguente modo
function fibBinet(n)
{
var n = parseInt(n);
if (isNaN(n))
{
alert("Indice non valido");
return 0;
}
if (n>70)
{
alert("Indice troppo grande");
return 0;
}
with (Math)
{
var rad5 = sqrt(5);
var Phi=(rad5+1)/2;
var psi=(1-rad5)/2;
return round((pow(Phi,n)-pow(psi,n))/rad5);
}
}
Altri algoritmi e altri linguaggi sono reperibili in Wikipedia