L'analogia tra il numero aureo Φ e il numero plastico P induce a chiedersi se anche per P non sia possibile definire una successione analoga a quella di Fibonacci, cioè una successione di numeri naturali da cui estrarre una successione di frazioni tendente a P.
Una prima soluzione al problema, proposta da R. Perrin e quindi nota come successione di Perrin, può essere individuata nel seguente modo.
Siano α, β e γ, con α reale e β e γ complessi coniugati con modulo < 1, le radici dell'equazione
![]()
cioè i numeri tali che
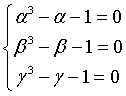
e sia pi la somma delle loro potenze con esponente i
![]()
Si ha immediatamente p0 = 3.
Si ha inoltre
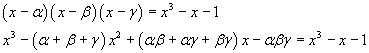
Per il principio di identità dei polinomi
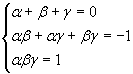
La somma delle prime potenze delle radici è uguale a 0, cioè p1 = 0.
La somma delle seconde potenze delle radici si può ottenere nel seguente modo
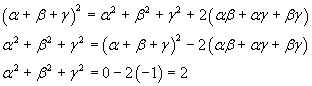
La somma delle seconde potenze delle radici è uguale a 2, cioè p2 = 2.
La somma delle terze potenze delle radici si può ottenere nel seguente modo
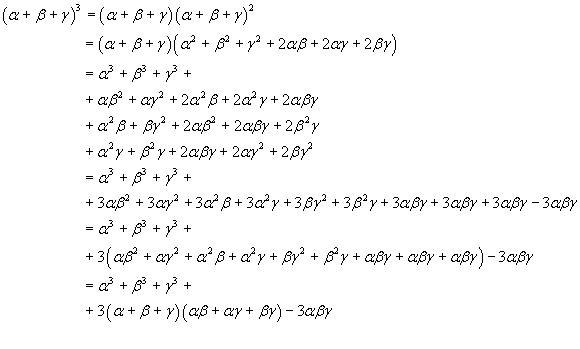
In definitiva
![]()
e, dato che la somma delle radici è 0 e il loro prodotto è 1,
![]()
La somma delle terze potenze delle radici è uguale a 3, cioè p3 = 3.
Si osserva inoltre che vale la seguente ricorsione
![]()
cioè che
![]()
Infatti, sommando le potenze di α si ha
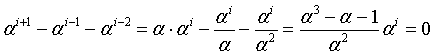
Stesso risultato si ottiene per le somme delle potenze di β e di γ.
Dati p0, p1, p2 e p3, la ricorsività permette di calcolare tutti i pi successivi
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ... |
| pi | 3 | 0 | 2 | 3 | 2 | 5 | 5 | 7 | 10 | 12 | 17 | 22 | 29 | 39 | 51 | 68 | 90 | 119 | 158 | 209 | 277 | ... |
Questa è la successione di Perrin e i suoi elementi sono detti numeri di Perrin.
L'uso della definizione ricorsiva per il calcolo informatico dell'ennesimo numero di Perrin è impraticabile. Meglio usare un ciclo, come nella seguente implementazione Javascript
function nPerrin(n)
{
n = parseInt(n);
var n1, n2, n3, p;
switch(n)
{
case 0: return 3;
case 1: return 0;
case 2: return 2;
default:
n1 = 2;
n2 = 0;
n3 = 3;
for (var i=3; i <= n; i++)
{
p = ( n2 + n3 );
n3 = n2;
n2 = n1;
n1 = p;
}
return(p);
}
}
Disponendo di Mathematica (Wolfram) si può definire la seguente funzione
PerrinN[n_]:=Switch[n,0,3,1,0,2,2,_,Module[{i,n1,n2,n3,val},n1=2;n2=0;n3=3;
For[i=3,i <= n,i++,val=n2+n3;n3=n2;n2=n1;n1=val];val]]
Table[PerrinN[n],{n,0,30}]
{3,0,2,3,2,5,5,7,10,12,17,22,29,39,51,68,90,119,158,209,277,367,486,644,853,1130,1497,1983,2627,3480,4610}
La successione di Perrin gode della seguente proprietà.
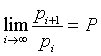
Infatti se α è la radice reale, cioè P, β e γ sono complessi coniugati con valore assoluto < 1 e le loro potenze tendono a 0 al crescere dell'esponente. Si ha quindi
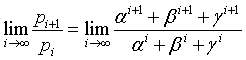
Dividendo numeratore e denominatore per αi
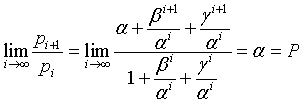
Il matematico francese E. Lucas notò un'interessante proprietà dei numeri di Perrin da lui analizzati: se l'indice i di un elemento pi della successione è primo, l'elemento è multiplo esatto dell'indice. Ad esempio:
| pi | 3 | 0 | 2 | 3 | 2 | 5 | 5 | 7 | 10 | 12 | 17 | 22 | 29 | 39 | 51 | 68 | 90 | 119 | 158 | 209 | 277 | ... |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ... |
| resto | 0 | 0 | 0 | 2 | 0 | 5 | 0 | 2 | 3 | 7 | 0 | 5 | 0 | 9 | 8 | 10 | 0 | 14 | 0 | 17 | ... |
Questa proprietà si può effettivamente dimostrare in modo generale.
Teorema: Se i è primo, i è un divisore di pi.
Se i è un numero primo, si ha
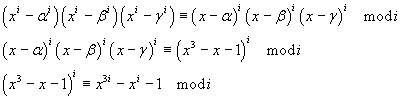
Per la transitività della congruenza in modulo i si ha quindi
![]()
Ma si ha anche
![]()
Uguagliando i coefficienti di x2i si ha quindi
![]()
cioè
![]()
In definitiva, se i è primo, lo i-esimo numero di Perrin è divisibile per i.
Ma ciò non implica il teorema inverso, cioè che se lo i-esimo numero di Perrin è divisibile per i allora i è primo.
Se valesse il teorema inverso, esso offrirebbe un valido test di primalità: per sapere se un numero è primo si controlla se è un divisore esatto del corrispondente numero di Perrin. Ma questa congettura è stata falsificata: esistono numeri divisibili per l'indice corrispondente che non sono primi: tali numeri sono chiamati pseudoprimi di Perrin. Ad esempio, p271441 è divisibile per 271441, ma 271441 non è primo: è il quadrato di 521; 271441 è quindi uno pseudoprimo di Perrin.
(Il calcolo di p271441 può essere effettuato dall'applicazione JS proposta ma può richiedere qualche minuto; potendo, provare con Mathematica.)