4. La successione di Padovan

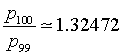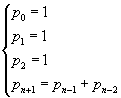
La ricerca di una successione di numeri naturali tali che il rapporto tra ognuno di essi e il precedente converga al numero plastico è stata affrontata anche dall'architetto Richard Padovan che ha scoperto che la successione p_n generata da

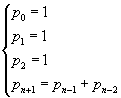
possiede caratteristiche analoghe a quella della successione di Perrin. La successione così definita è detta successione di Padovan e i suoi termini numeri di Padovan.

I numeri di Padovan p_i possono essere dedotti nel seguente modo.

1. Si esprime p_i come combinazione lineare delle potenze i-esime delle radici α, β e γ dell'equazione x³-x-1 = 0, con α reale e β e γ complessi coniugati con valore assoluto < 1:
   
2. Assumendo p₀, p₁ e p₂ tutti uguali a 1, si ha
   
3. Risolvendo il sistema
   
4. quindi
   

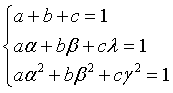
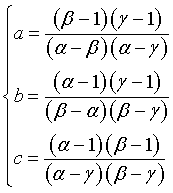
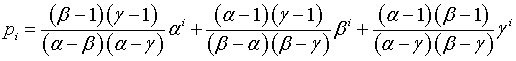
Questa definizione di p_i implica

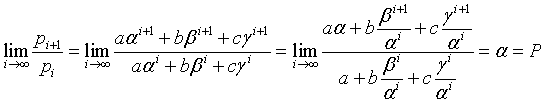
poiché per esponente tendente ad infinito, le potenze di β e γ tendono a 0.

Si ha inoltre

cioè

Infatti

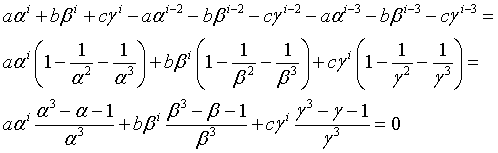
L'uso della definizione ricorsiva per il calcolo informatico dell'ennesimo numero di Padovan è impraticabile. Meglio usare un ciclo, come nella seguente implementazione Javascript

function nPadovan(n)
{
  n = parseInt(n);
  if (n < 2) return 1;
  var n1 = 1;
  var n2 = 1;
  var n3 = 1;
  var p;
  for (var i=3; i<=n; i++)
    {
      p = n2 + n3;
      n3 = n2;
      n2 = n1;
      n1 = p;
    }
  return(p);
}

Disponendo di Mathematica (Wolfram) si può definire la seguente funzione

PadovanN[n_]:=Switch[n,0,1,1,1,2,1,_,Module[{i,n1,n2,n3,val},n1=1;n2=1;n3=1;
      For[i=3,i <= n,i++,val=n2+n3;n3=n2;n2=n1;n1=val];val]]
 Table[PadovanN[n],{n,0,30}]
 {1,1,1,2,2,3,4,5,7,9,12,16,21,28,37,49,65,86,114,151,200,265,351,465,616,816,1081,1432,1897,2513,3329}

In generale, ogni successione di numeri q_i espressi come combinazione lineare di coefficienti a, b, c delle potenze i-esime delle radici α, β e γ, dati tre arbitrari valori per q₀ , q₁ e q₂, gode della stessa ricorsione e il rapporto tra ogni termine e il precedente converge a P.

Ad esempio, la successione

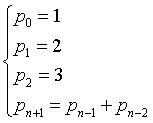
cioè

è tale che