(a cura di R. Bigoni)
Un insieme S di n elementi può essere suddiviso in k parti pi tali che
Ognuna di queste possibili suddivisioni è detta partizione di S.
Se gli elementi di S sono tutti distinguibili, il numero delle delle sue partizioni in k parti (o k-partizioni)
è indicato con il simbolo
![]() ,
proposto dal matematico serbo Jovan Karamata in analogia con il simbolo usato per i coefficienti binomiali,
è detto numero di Stirling di seconda specie, dal nome
del matematico scozzese J. Stirling
,
proposto dal matematico serbo Jovan Karamata in analogia con il simbolo usato per i coefficienti binomiali,
è detto numero di Stirling di seconda specie, dal nome
del matematico scozzese J. Stirling
Dato n, risultano immediate le seguenti identità:
![]()
Infatti, sia s un qualunque elemento di S e Cs l'insieme complementare del singoletto {s} rispetto a S; il numero di tutti i possibili sottinsiemi Σi non vuoti di Cs è 2n-1-1; ogni Σi individua una bipartizione di S data da Σi e dal suo complementare rispetto a S.
![]()
Infatti in questo caso il numero delle partizioni coincide il numero delle coppie di elementi di S; una partizione formata da una coppia e dai singoletti degli n-2 elementi rimanenti è una partizione in n-1 parti.
Si ottengono immediatamente i seguenti valori:
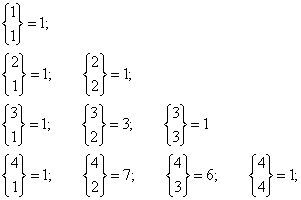
Per n > 1, scelto in S un elemento s, le k-partizioni di S risultano di due tipi:
Sia C il complementare di {s} rispetto a S.
Le partizioni di tipo X sono
![]() in quanto ogni (k-1)-partizione di C unita al singoletto {s} genera una k-partizione di
S.
in quanto ogni (k-1)-partizione di C unita al singoletto {s} genera una k-partizione di
S.
Le partizioni di tipo Y sono ![]() ,
poiché unendo ogni k-partizione di C con il singoletto {s} si ottiene una
k-partizione di S.
,
poiché unendo ogni k-partizione di C con il singoletto {s} si ottiene una
k-partizione di S.
Assumendo
![]()
si ottiene
![]()
Per n>1, la (1,1) permette di ricavare ricorsivamente i numeri di Stirling.
Per n=5:
![]()
La seguente applicazione Javascript permette di ottenere i numeri di Stirling di seconda specie (per grandi numeri il tempo di calcolo può risultare eccessivo).
Per grandi numeri si può usare WolframAlpha.

Scrivendo in righe successive i numeri di Stirling per n e k crescenti, si ottiene il triangolo di Stirling.
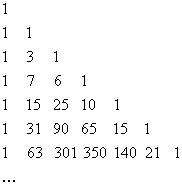
Si può ottenere direttamente il valore di
![]() usando i polinomi di Grunert. Data una funzione continua f(x), si definisce
l'operatore G
usando i polinomi di Grunert. Data una funzione continua f(x), si definisce
l'operatore G
![]()
Se f(x)=ex, si ha
![]()
Applicando successivamente G all'esito dell'applicazione precedente, si ottiene
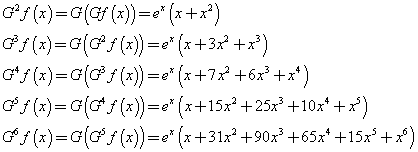
I polinomi che moltiplicano l'esponenziale sono i polinomi di Grunert.
I coefficienti dei polinomi di Grunert coincidono con i numeri di Stirling di seconda specie: non è un caso. In essi effetti si formano nello stesso modo ricorsivo. Infatti, indicando con gnk i coefficienti del polinomio di Gn, si ha
![]()
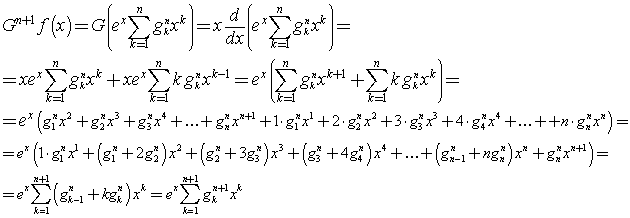
quindi
![]()
La formazione dei coefficienti gn,k coincide con la (1.1), dunque
![]()
Se si applica ripetutamente l'operatore G allo sviluppo dell'esponenziale naturale in serie di Maclaurin
![]() si ottiene
si ottiene
![]()
Uguagliando le due espressioni di Gn si ottiene
![]()
![]()
![]()
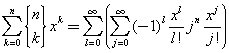
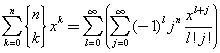
La sommatoria a secondo membro è una sommatoria sulle potenze crescenti di x con esponenti l+j. Poiché la sommatoria a primo membro è finita, con k da 0 a n, si assume
![]()
quindi
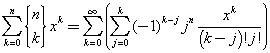
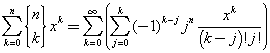
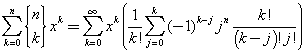
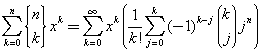
Confrontando le sommatorie a primo e a secondo membro si ottiene
![]()
Questa equazione connette i numeri di Stirling di seconda specie con i coefficienti binomiali e ne permette un calcolo più rapido.
Poiché ![]() , dalla (1.2)
si ricava immediatamente
, dalla (1.2)
si ricava immediatamente
![]()
Moltiplicando entrambi i membri della (1.3) per (-1)n
![]()
Le potenze (-1)2n-j sono identiche alle potenze (-1)j, dunque
![]()
Se gli n elementi di S sono tutti distinguibili, il numero delle delle sue partizioni è dato dalla somma di tutti i numeri di Stirling di seconda specie con k da 1 a n. Questo numero è noto come numero di Bell Bn, dal nome del matematico e romanziere E. T. Bell.
![]()
I numeri di Bell possono essere ottenuti ricorsivamente con la seguente procedura
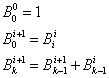
cioè
per ogni nuova riga:
Si forma così il triangolo di Bell
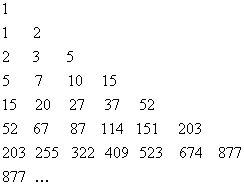
I numeri nella colonna di ordine 0 sono i numeri di Bell
La seguente applicazione Javascript permette di ottenere i numeri di Bell (per grandi numeri il tempo di calcolo può risultare eccessivo).
Per grandi numeri si può usare WolframAlpha.
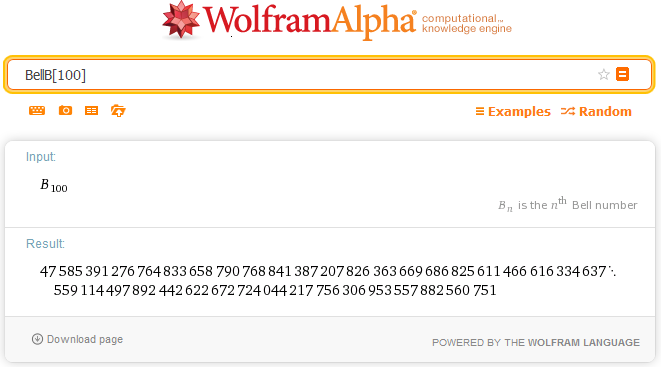
In questo sito l'applicazione Javascript SuperCalcolatrice permette il calcolo dei numeri di Bell.
Se gli n elementi di un insieme S sono tutti indistinguibili l'uno dall'altro, il numero delle sue partizioni si riduce drasticamente rispetto a quello calcolato dal numero di Bell.
Infatti, se, ad esempio, si considera un insieme I = {a,b,c,d} il numero delle sue partizioni è B4 = 15. Se invece si considera un insieme S = {a,a,a,a} da esso si possono ricavare le seguenti partizioni:
quindi il numero delle sue partizioni è 5.
Il calcolo del numero delle partizioni di un insieme di n elementi indistinguibili coincide con il calcolo del numero di modi in cui il numero naturale n può essere scritto come somma di addendi naturali positivi ≤ n. Quindi il termine partizione può essere importato dalla teoria degli insiemi a quella dei numeri naturali.
Dato un numero naturale positivo n, si dice partizione Λn,k di n una successione non decrescente di numeri naturali positivi λn,i ≤ n
![]()
tali che
![]()
Ovviamente il massimo valore di k, cioè n, si ha nel caso in cui tutti i λn,i sono uguali a 1.
È ovvio che il numero 1 ammette la sola partizione ![]() .
.
Il numero 2 ammette due partizioni:
![]()
Il numero 3 ammette tre partizioni:
![]()
Il numero 4 ammette 5 partizioni:
![]()
Il numero 5 ammette 7 partizioni:
![]()
Dato un qualunque naturale positivo n, il numero p(n) delle sue possibili partizioni è detto funzione di partizione.
Dagli esempi proposti si desume
Come si può vedere nella bibliografia allegata alla pagina di Mathworld già citata, numerosi matematici hanno studiato le proprietà della funzione di partizione, in particolare con l'obiettivo di individuare algoritmi che permettano la determinazione del suo valore per un qualunque argomento n.
Un primo importante risultato fu la formula ricorsiva di Eulero, per la quale, in un modo che ricorda la ricorsione che genera i numeri di Fibonacci, p(n), si ottiene dai valori p(ni ) di tutti i numeri ni che si ottengono sottraendo da n i numeri pentagonali generalizzati ωi≤n. Si assume p(0)=1.
L'insieme Ω dei numeri pentagonali generalizzati ωi si ottiene dall'unione delle successioni
di naturali
![]() definite nel seguente modo
definite nel seguente modo
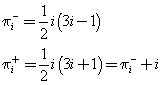
Se, ad esempio, n=10, i numeri ni che si ottengono sottraendo da 10 i n. pentagonali generalizzati ωi ≤10 sono:
La formula ricorsiva di Eulero stabilisce che, fissato il massimo indice iM per i numeri ni
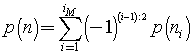
dove (i-1):2 rappresenta il quoziente intero di i-1 diviso 2
In pratica, nella sommatoria si alternano due termini positivi con due termini negativi.
La formula di Eulero è ricorsiva perché il calcolo di p(n) è possibile solo se si sono prima calcolati tutti i possibili valori p(ni ) i quali, a loro volta, possono essere ricavati con la stessa formula.
Riprendendo l'esempio precedente
p(10) = p(9) + p(8) - p(5) - p(3)
Bisogna quindi calcolare p(9), p(8), p(5) e p(3)
Per la formula di Eulero
Per calcolare p(10) è utile che siano noti tutti i valori da p(0) a p(9).
In generale, per calcolare p(n) è utile che siano noti tutti i valori da p(0) a p(n-1).
Il numero di questi valori coincide con il numero dei pentagonali estesi ≤ n.
La seguente applicazione Javascript permette di ottenere i valori di p(n) (per grandi numeri il tempo di calcolo può risultare eccessivo).
Applicazioni come WolframAlpha permettono il calcolo dei valori di p(n) senza limiti di range.
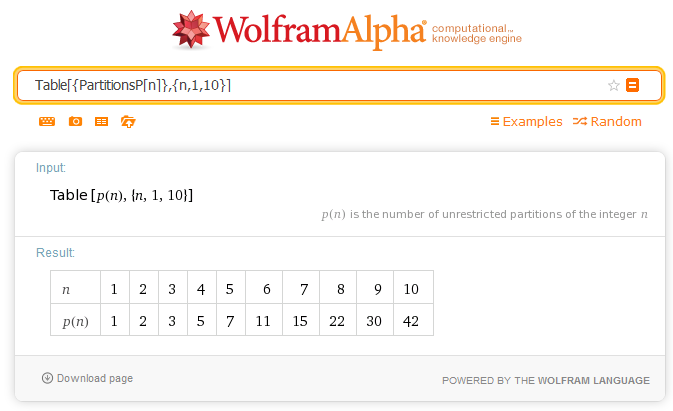
Come si vede dalla figura, p(n) cresce rapidamente al crescere di n. Ad esempio, p(1000)=24061467864032622473692149727991 usando WolframAlpha, in cui il valore di p(n) è dato dalla funzione PartitionsP[n] di Mathematica e in cui si può cambiare a piacere il valore dell'argomento.
Per valori molto grandi di n sono stati messi a punto algoritmi più efficaci. Ad esempio, Mathematica usa il metodo di Hardy- Ramanujan- Rademacher. Recentemente il matematico Ken Ono ha fornito nuovi importanti contributi.
ultima revisione: Giugno 2020