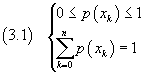
Se il campione è un insieme ordinato di n valori reali discreti xk che possono essere attribuiti alla variabile reale x, una funzione reale p(xk) tale che
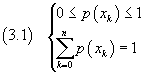
è detta distribuzione discreta di probabilità e x è detta variabile casuale o stocastica o aleatoria.
Per semplificare l'esposizione, in questa pagina si pone
![]()
quindi
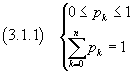
Data una distribuzione discreta di probabilità, se ne possono rappresentare le caratteristiche globali usando due importanti descrittori detti media (o valor medio) e varianza.
La media è data da
![]()
Se si rappresenta con ξk lo scarto del valore xk dalla media,
![]()
la varianza, espressa da σ2 è la media dei quadrati degli scarti:
![]()
La radice quadrata della varianza è detta deviazione standard della popolazione:
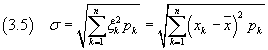
La deviazione standard è un altro importante descrittore in quanto esprime la dispersione dei valori xk attorno alla media: la dispersione cresce al crescere di σ.
Teorema: La varianza è data dalla differenza tra la media dei quadrati e il quadrato della media.
![]()
Dimostrazione:
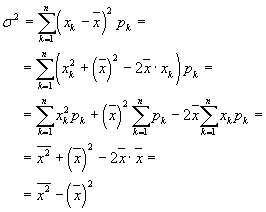
Se gli n valori pk sono tutti uguali, la distribuzione è detta uniforme.
Dalla seconda delle (3.1) si ha
![]()
In particolare, se xk=k, la media è
![]()
Si è applicata l'uguaglianza
![]()
nota dalla teoria delle progressioni aritmetiche.
Per la (3.6), in questo caso la varianza è
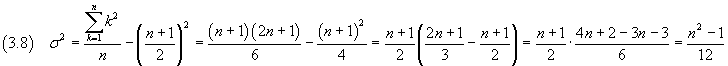
Si è applicata l'uguaglianza
![]()
ottenuta per induzione.
La deviazione standard è
![]()
Esempio
Nel lancio di un dado ognuno dei sei punti k ha probabilità
![]() .
.
Il valor medio è
![]()
La varianza è
![]()
e la deviazione standard
![]()
Dato il numero n di prove e la probabilità p, la funzione pk=Pn,k nella (2.9) rappresenta distribuzione di probabilità di una variabile casuale k che può assumere valori interi da 0 a n: infatti si constata facilmente che questa funzione verifica le condizioni (3.1.1). In particolare, dato che per ipotesi p+q=1,
![]()
Questa distribuzione di probabilità è detta distribuzione binomiale o distribuzione bernoulliana.
Applicando la (3.2), il valor medio della variabile casuale binomiale k in n prove è
![]()
Se si sviluppa il secondo membro si ha
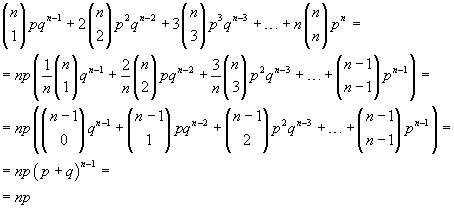
e infine
![]()
Inoltre si ha
![]()
Lo sviluppo del secondo membro dà
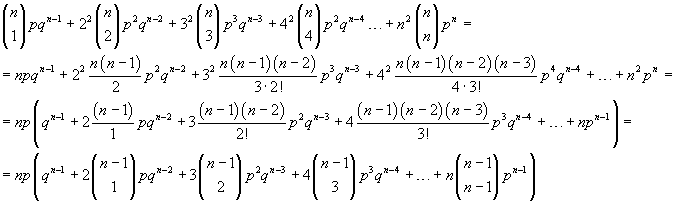
L'espressione tra parentesi può essere suddivisa in due somme
![]()
![]()
s2 è il valor medio della variabile casuale binomiale k in n-1 prove, quindi dalla (3.10),
![]()
Si ottiene così
![]()
e infine
![]()
![]()
La seguente applicazione JS calcola le caratteristiche di una distribuzione binomiale.
La probabilità p può essere scritta come decimale (< 1) o come frazione propria.
Le probabilità in ordinata sono espresse in percentuale.
Per vedere tabelle e grafici bisogna permettere al proprio browser di mostrare i popup.
Se il browser non permette frames interni, potete accedere direttamente alla pagina dell'applicazione.
Se p tende a 0 e n tende all'infinito, la distribuzione binomiale converge alla distribuzione di Poisson.
In questo caso, se λ rappresenta il valor medio della distribuzione, si ha
![]()
L'uguaglianza (3.14) può essere ottenuta nel seguente modo:
![]()
![]()
Dalla (2.9) si ha
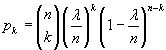
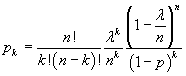
Se n→∞ e p→0
![]()
![]()
![]()
quindi ![]()
Se p→0, q→1, quindi, dalla (3.12),
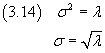
La seguente applicazione JS, in una distribuzione di Poisson di media λ prefissata, calcola la probabilità che un evento si verifichi k volte.
La media λ può essere scritta come decimale o come frazione. Per vedere le tabelle bisogna permettere al proprio browser di mostrare i popup.
Se il browser non permette frames interni, potete accedere direttamente alla pagina dell'applicazione.
La seguente applicazione JS rappresenta una distribuzione di Poisson di media λ prefissata.
La media λ può essere scritta come decimale o come frazione.
Le probabilità in ordinata sono espresse in percentuale.
Per vedere le tabelle bisogna permettere al proprio browser di mostrare i popup.
Se il browser non permette frames interni, potete accedere direttamente alla pagina dell'applicazione.