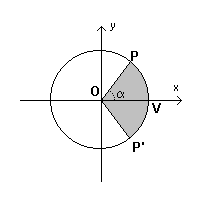
Dato nel piano cartesiano Oxy il grafico della circonferenza γ con centro nell'origine O e raggio
unitario, la cui equazione è
,
siano V il punto in cui γ intercetta il semiasse positivo delle ascisse e P(x;y) un suo punto qualunque.
Le coordinate x e y di P sono funzioni dell'angolo VOP di misura α e, se questa misura è in radianti,
anche della lunghezza dell'arco VOP che ha misura numericamente identica a α.
Se si indica con P' il punto di γ simmetrico di P rispetto all'asse delle ascisse, anche l'area del settore circolare P'OP coincide numericamente con α. Si possono quindi interpretare le coordinate di P come funzioni parametriche dell'area del settore circolare P'OP.
Queste funzioni sono dette rispettivamente coseno circolare (o più semplicemente coseno) e seno circolare (o più semplicemente seno) di α.
Quindi
e, dall'equazione di γ,
Il rapporto tra seno e coseno è detto tangente circolare
(o più semplicemente tangente)
Dalle definizioni di seno e coseno si ha
Il coseno è una funzione pari, mentre il seno e la tangente sono funzioni dispari, quindi il grafico del coseno è simmetrico rispetto all'asse delle ordinate, i grafico del seno e della tangente sono simmetrici rispetto all'origine.
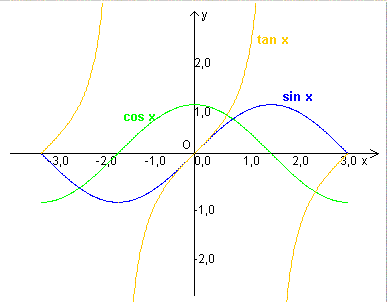
Inoltre, per ogni numero intero k,
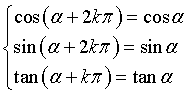
cioè seno, coseno e tangente, sono funzioni periodiche con periodo 2π per il seno e il coseno e π per la tangente.
La seguente applicazione Javascript permette il calcolo dei valori delle tre funzioni. L'argomento può essere espresso in forma sessagesimale o come reale.
Se l'argomento è reale si intende in radianti. È possibile esprimere l'argomento come multiplo o sottomultiplo di π che va immesso come P.
Se il browser attivo non accetta il tag iframe è possibile accedere direttamente alla pagina.
Quanto più P si avvicina a V, tanto più il settore circolare P'OP diventa indistinguibile da un triangolo isoscele di altezza OV=1 e base PP' = 2sinα. In un triangolo il rapporto tra il doppio dell'area e la base è uguale all'altezza, per cui
Se si muove il punto P(x;y) in senso antiorario lungo γ spazzando un angolo β,
si arriva al punto Q(X;Y) of γ, tale che
, dove
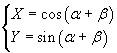
Se si applica alle coordinate del punto P(x;y) di γ la trasformazione
si ottiene proprio
, quindi la trasformazione (1.5)
trasforma il punto P nel punto Q.
In generale, trasformazioni del tipo (1.5) trasformano una circonferenza in se stessa. Queste trasformazioni sono dette rotazioni.
Si ottiene
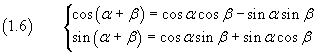
Le (1.6) sono le formule di addizione per il coseno e per il seno.
Formule di addizione con WolframAlpha.
Dalle formule di addizione si possono agevolmente ottenere altre utili identità, come le formule di duplicazione
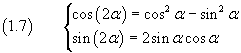
Formule di duplicazione con WolframAlpha.
Dalle formule di addizione si ottengono anche le formule di prostaferesi (o formule di Simpson)
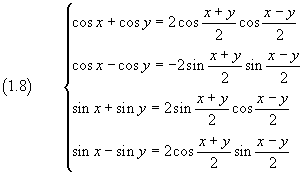
Formule di prostaferesi con WolframAlpha
La derivata di sin x rispetto a x, per definizione, è
Per la quarta formula di prostaferesi il numeratore è
quindi
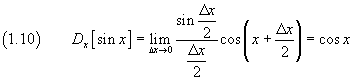
La derivata di cos x rispetto a x, per definizione, è
Per la seconda formula di prostaferesi il numeratore è
quindi
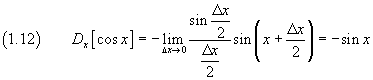
La derivata di tan x rispetto a x, si ottiene derivando il rapporto tra seno e coseno
Seno e coseno hanno come dominio l'insieme dei reali ℜ e codominio [-1;1] e sono periodiche dunque non sono funzioni biunivoche. Si possono definire le loro funzioni inverse solo restringendo il loro dominio a un sottinsieme in cui siano strettamente crescenti o decrescenti.
Il seno è strettamente crescente in [-π/2;π/2], dunque in questo dominio
y è reale solo se |x| ≤ 1.
Si ha
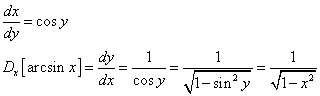
Il coseno è strettamente decrescente in [0;π], dunque in questo dominio
y è reale solo se |x| ≤ 1.
Si ha
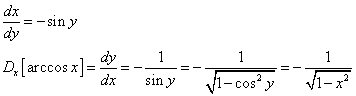
La tangente è strettamente crescente in [-π/2;π/2], dunque in questo dominio
y è reale ∀ x ∈ ℜ
Si ha
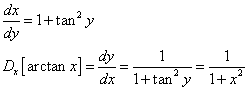
Note le derivate delle funzioni circolari dirette e inverse, è immediatamente possibile risalire alle antiderivate delle derivate, cioè ottenere gli integrali indefiniti delle derivate.
