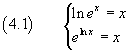
La funzione esponenziale naturale è definita per ogni x ∈ R ed è sempre crescente, quindi è biunivoca quindi invertibile. Esiste cioè una funzione, che potrebbe essere provvisoriamente chiamata invexp(x) tale che invexp(exp(x))=x.
Il dominio di invexp(x) coincide con il codominio di exp(x), quindi invexp(x) può essere applicata solo a numeri reali positivi.
La funzione invexp(x) è comunemente detta logaritmo naturale (o semplicemente logaritmo) e abbreviata in ln (talora anche in log).
Quindi, per definizione,
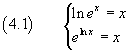
Se
allora
,
cioè le uguaglianze
e
sono perfettamente equivalenti: esse rappresentano la stessa relazione tra x and y.
In particolare, da
si ottiene
e da
si ottiene
.
Dalla seconda delle (4.1) si ottiene
Applicando la derivazione a catena delle funzioni composte si ha
e infine
Le uguaglianze
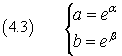
sono equivalenti a
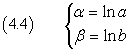
Moltiplicando membro a membro le (4.3) risulta
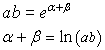
e, dalle (4.4)
Il logaritmo di un prodotto è uguale alla somma dei logaritmi dei singoli fattori.
Questa proprietà può essere facilmente estesa ad un numero qualunque di fattori.
Da
si ottiene
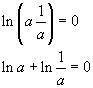
Il logaritmo del reciproco di un numero è uguale all'opposto del logaritmo del numero stesso.
Applicando le due proprietà precedenti si ha
Il logaritmo del rapporto tra due numeri è uguale alla differenza tra i loro logaritmi.
Dato
si ha
e, elevando entrambi i termini a
,
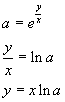
quindi
Il logaritmo di una potenza è uguale al prodotto tra l'esponente e il logaritmo della base.
Il logaritmo di un radicale è uguale al rapporto tra il logaritmo del radicando e l'indice del radicale.