La funzione
![]()
non è definita per x=0, ma questa singolarità è eliminabile perché il limite per x→0 è finito, come si può facilmente verificare applicando la regola di De L'Hôpital. La stessa cosa vale per le sue derivate:
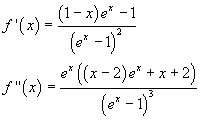
Si può quindi sviluppare questa funzione in serie di MacLaurin
![]()
dove Bn è il limite per x→0 della derivata n-sima di f(x):
![]()
In questo modo si ottiene:
![]()
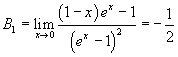
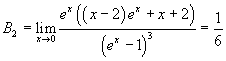
e così via. I coefficienti Bn sono detti numeri di Bernoulli, da nome del matematico che per primo ne fece uso nella sua Ars conjectandi, un trattato sulla teoria della probabilità.
Il calcolo delle derivate e dei loro limiti è lento e laborioso e non fornisce indicazioni su eventuali relazioni tra i coefficienti Bn che ne permettano un calcolo più diretto. Un'alternativa a questo metodo può essere trovata nel seguente modo.
Da
![]() si ottiene
si ottiene
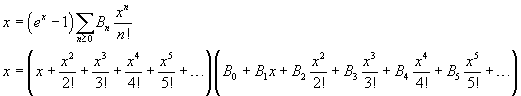
Si sviluppa il prodotto a secondo membro
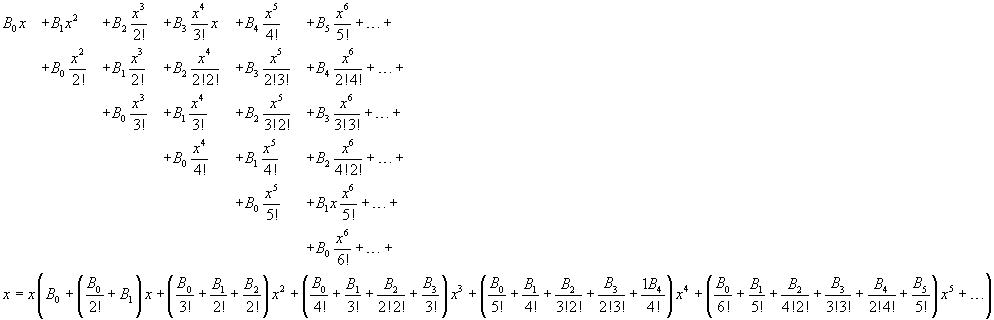
Per il principio di identità dei polinomi, il primo e secondo membro sono uguali solo se nel secondo membro B0=1 e i coefficienti delle potenze di x sono nulli. Quindi
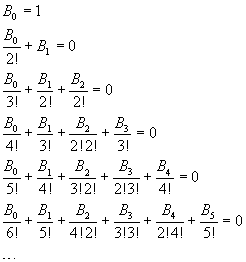
I denominatori delle frazioni nei secondi membri coincidono con i denominatori delle espressioni fattoriali dei coefficienti binomiali.
![]()
La n-sima riga della successione indicata è quindi data da
![]()
Se, per esempio, si considera l'ultima tra le righe calcolate, si ha
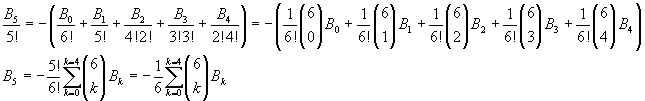
In generale, si ha
![]()
Questa relazione permette il calcolo ricorsivo dei coefficienti Bn
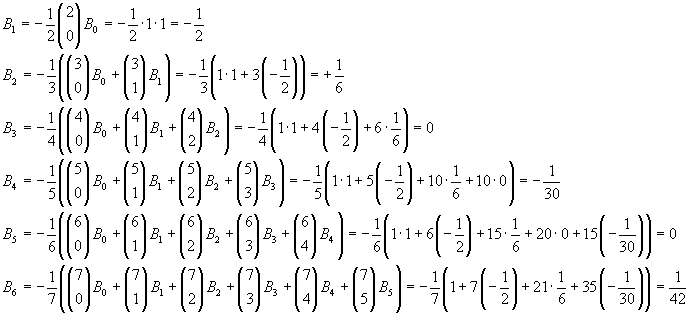
Per ottenere ulteriori valori di Bn, conviene automatizzare il calcolo come nella seguente applicazione Javascript.
Se il vostro browser non ammette il tag iframe potete aprire la pagina sorgente
Numeri di Bernoulli con WolframAlpha
Dai valori precedentementi calcolati e usando l'applicazione JS si può congetturare che tutti i numeri di Bernoulli con indice dispari ≥ 3 sono nulli. Questo è vero perché da
![]()
si ottiene
![]()
e poi
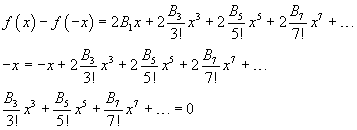
Quindi ogni B nel primo membro deve essere nullo.
Data la funzione
![]()
siano En i valori assunti da essa e dalle sue derivate successive per x=0. I valori En sono detti numeri di Eulero. Si ha quindi
![]()
da cui
![]()
Rappresentando esplicitamente alcuni degli addendi dei fattori a secondo membro
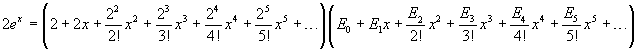
Sviluppando il prodotto a secondo membro
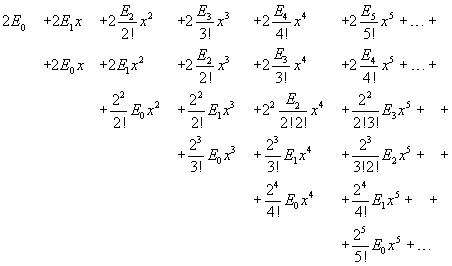
Si ottiene quindi
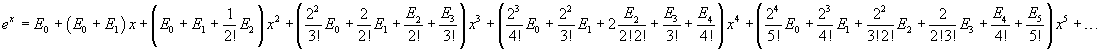
Per il principio di identità dei polinomi i coefficienti delle potenze di x a secondo membro devono coincidere con i coefficienti dello sviluppo in serie dell'esponenziale. Questa identità permette di calcolare ricorsivamente i valori di En. Infatti
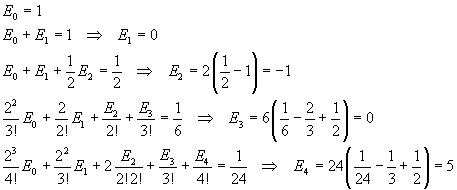
Ovviamente E5, come E1 e E3 è 0 perché tutti gli En con n dispari sono nulli, dato che la s(x) è una funzione pari. L'identità tra i coefficienti delle quinte potenze può essere utile per congetturare un metodo di calcolo generale.
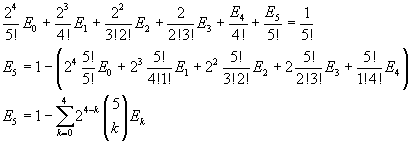
Si può congetturare che in generale
![]()
Per ottenere i valori di En, conviene automatizzare il calcolo come nella seguente applicazione Javascript.
Se il vostro browser non ammette il tag iframe potete aprire la pagina sorgente
Esistono varie convenzioni sulla notazione dei numeri di Eulero. Qui si assume la convenzione adottata in Mathematica
per la funzione EulerE[n].