11. Sviluppo in serie di Fourier.

Nel paragrafo precedente si è visto come una funzione φ_n dello spazio vettoriale Φ_n può essere espressa come

Le funzioni di Φ_n (definite nell'intervallo [-π;π]) hanno le seguenti proprietà:

• il loro valore medio integrale è nullo;
• sono continue e derivabili in [-π;π].

Se il valore di n è finito, Φ_n non comprende tutte le possibili funzioni con queste caratteristiche. Si può però congetturare che, all'aumentare di n, l'insieme Φ_n tenda a coincidere con l'insieme Φ di tutte le funzioni periodiche φ(x) di periodo 2π, continue, derivabili e di valor medio nullo in [-π;π], cioè che

con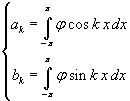

La congettura può essere generalizzata ed applicarsi all'insieme P di tutte le funzioni (reali di variabile reale) periodiche p(x) di periodo 2π, continue, derivabili e di valor medio ottenendo

Quest'ultima relazione, ideata da J. Fourier, è oggi nota come sviluppo in serie di Fourier ed è stata teoricamente convalidata dal lavoro di numerosi matematici dell'Ottocento e del Novecento, che ne hanno dimostrato l'applicabilità anche a classi di funzioni periodiche sottoposte a condizioni meno restrittive di quelle qui proposte.

Questo sviluppo in serie può essere facilmente adattato a funzioni periodiche di periodo qualunque 2L con la sostituzione di variabile desumibile dalla proporzione .

Se un funzione p(x) è dispari, tutti i coefficienti a_k sono nulli e sono da calcolare esplicitamente solo i coefficienti b_k.

La seguente applicazione Javascript permette di osservare come, al crescere del numero di armoniche, cioè del numero di termini nella sommatoria, questa approssima sempre più la funzione p(x) = x.
Le ascisse x_A e x_B sono multiple di π.
L'applicazione, come le seguenti, funziona appropriatamente solo se il vostro browser permette i popup.

Se un funzione p(x) è pari, tutti i coefficienti b_k sono nulli e sono da calcolare esplicitamente solo i coefficienti a_k.

Lo sviluppo di un polinomio si ottiene sommando gli sviluppi dei suoi monomi.

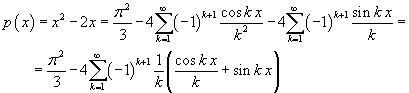
La seguente applicazione Javascript permette di osservare come, al crescere del numero di armoniche, cioè del numero di termini nella sommatoria, questa approssima sempre più la funzione p(x) = x²-2x.
Le ascisse x_A e x_B sono multiple di π.