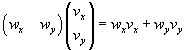
Dato il vettore v(x;y), si dice prodotto di v per un numero reale a il vettore r(ax;ay).
Un insieme di vettori reali in cui è definito il prodotto per un numero reale è uno spazio vettoriale (o spazio lineare) In questo contesto un numero reale è denominato scalare.
Dati due vettori w(wx;wy) e v(vx;vy) si dice prodotto scalare v·w il numero reale wxvx+wyvy.
Il prodotto scalare dei vettori w(wx;wy) e v(vx;vy può essere efficacemente rappresentato nel seguente modo
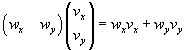
in cui il vettore w è rappresentato da una matrice riga e il vettore v è rappresentato da una matrice colonna. Il prodotto scalare si ottiene moltiplicando ordinatamente ogni elemento del vettore riga per ogni elemento del vettore colonna.
Adottando una notazione e una terminologia proposta da
P.A.M. Dirac le matrici riga sono
rappresentate da
vettori bra (scritti <w|) e le matrici colonna da vettori
ket (scritti |v>) nel seguente modo:
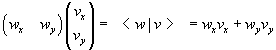
La radice quadrata del prodotto scalare del vettore v per se stesso può essere assunta come norma di v e indicata nel seguente modo:
![]()
Nel prodotto scalare di un vettore L1(L1,1;L1,2) per un vettore v(x,y) di ℜ2
![]()
L1 può essere interpretato come un operatore che, applicato al vettore v, gli fa corrispondere in modo univoco il numero reale
![]()
Per fare corrispondere ad ogni vettore v(x;y) una coppia di numeri reali che possano essere interpretati come componenti di un vettore v’(x’;y’), univocamente corrispondente a v, è necessario accoppiare il primo operatore L1 con un secondo operatore L2(L2,1;L2,2) tale che
![]()
La coppia ordinata L dei due operatori L1 e L2 può essere complessivamente rappresentata da una matrice quadrata di due righe e due colonne (secondo ordine)
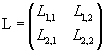
detta matrice dell'operatore L. In generale, nel seguito, quando non ci siano ambiguità, si userà lo stesso simbolo L per l'operatore e per la sua matrice.
L è un operatore che fa corrispondere in modo univoco al vettore v(x;y) il vettore v’(L1,1x+L1,2y; L2,1x+L2,2y):
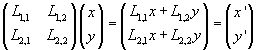
Più sinteticamente si può scrivere
![]()
e si interpreta tale scrittura dicendo che l'applicazione dell'operatore L al vettore v produce il vettore v’ o, più semplicemente, che il prodotto di L per v dà v’.
Risulta quindi che il prodotto di un operatore L per un vettore v è un vettore le cui componenti si ottengono moltiplicando ordinatamente gli elementi di ogni riga della matrice dell'operatore L per gli elementi del vettore.
Si dice anche che L trasforma il vettore v nel vettore v’.
L'operatore L possiede le seguenti proprietà (a è uno scalare)
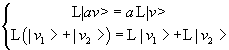
Tutti gli operatori (come ad esempio gli operatori di derivazione e di integrazione) che, come L, possiedono tali proprietà, sono detti operatori lineari.
L'operatore I di matrice
![]()
è tale che moltiplicato per qualunque vettore dà il vettore stesso. L'operatore I è detto Identità.