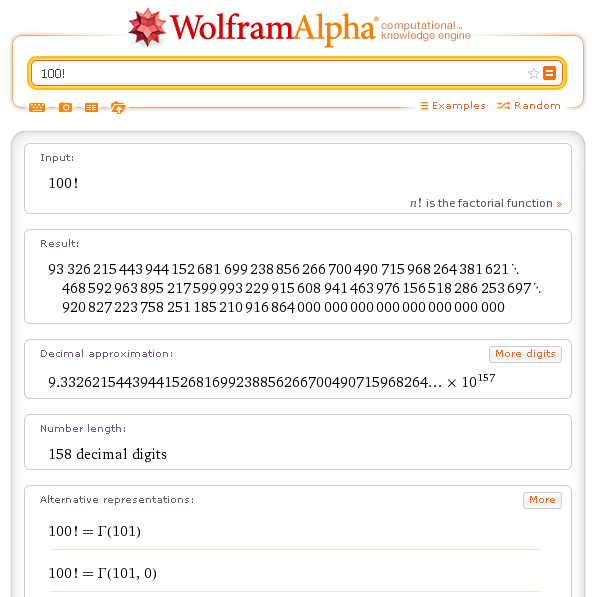
Il modo più semplice di lavorare con Mathematica è di usarlo come una supercalcolatrice, in grado di svolgere calcolo numerico esatto ed approssimato a qualunque grado di precisione richiesto dall'utente.
Il calcolo sugli interi è sempre esatto e completo, a differenza di quanto avviene nelle calcolatrici tascabili che per interi molto grandi passano forzatamente alla notazione esponenziale con mantissa approssimata.
| Mathematica | risultato | esempio |
|---|---|---|
| Prime[n] | calcola lo n-esimo numero primo | Prime[10] |
| PrimeQ[n] | controlla se n è un numero primo | PrimeQ[1234567] |
| Divisors[n] | produce la lista dei divisori di n | Divisors[1234567] |
| FactorInteger[n] | produce la scomposizione di n in potenze di fattori primi | FactorInteger[1234567] |
| Quotient[m,n] | calcola quante volte n è contenuto in m | Quotient[100,7] |
| Mod[m,n] | calcola il resto della divisione di m per n | Mod[100,7] |
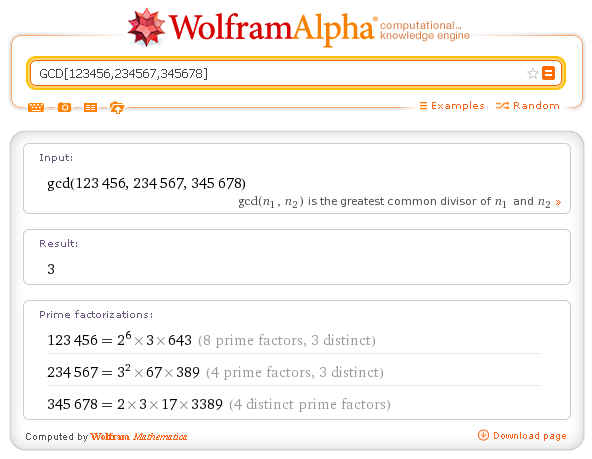
| GCD[i,j,k,m,n,...] | calcola il Massimo Comun Divisore dei numeri in lista | GCD[30,120,45] |
| LCM[i,j,k,m,n,...] | calcola il Minimo Comune Multiplo dei numeri in lista | LCM[30,120,45] |
| Factorial[n] | calcola il fattoriale di n (più comodo n!) | Factorial[10]; 10! |
| Factorial2[n] | calcola il doppio fattoriale di n (più comodo n!!) | Factorial2[10]; 10!! |
| Binomial[n,k] | calcola il coefficiente binomiale (nk) | Binomial[10,4] |
| Fibonacci[n] | calcola lo n-esimo numero di Fibonacci | Fibonacci[50] |
| BaseForm[n,b] | rappresenta in numero n in base b | BaseForm[1024,2] |
Esempi

Liste di oggetti possono essere prodotte con l'uso dell'operatore Table.
L'argomento di Table è costituito da due oggetti: una funzione di una o più variabili e una o più liste il cui primo elemento è la variabile che può essere seguita o dall'ultimo valore assumibile (il primo è di default 1) o dal primo e ultimo valore assumibili. In questo modo la variabile (ad esempio n che in questo caso è un semplice contatore) viene incrementata di una unità ad ogni passo.
Esempio.

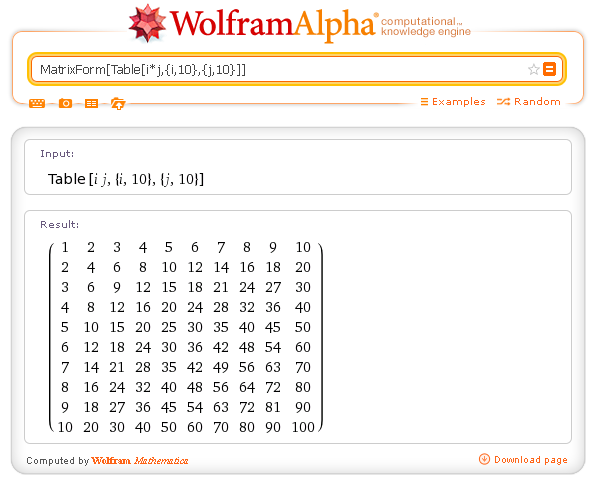
L'operatore Table può essere modulato dall'operatore MatrixForm che formatta l'output su più righe incolonnate.
Esempio: la tabella pitagorica.
Esempio: il triangolo di Pascal (o Tartaglia).

In questo ultimo esempio si è usata la funzione If che richiede tre argomenti: una condizione,il valore se la condizione è vera, il valore se la condizione è falsa.
Nel calcolo sui razionali e sui real Mathematica tende sempre a produrre il risultato esatto di una espressione e fornisce una approssimazione decimale solo se utile o espressamente richiesta.
In generale, operando su interi e frazioni, si ottengono frazioni ridotte ai minimi termini.
Numerator e Denominator dànno numeratore e denominatore di una frazione.
Esempi
WolframAlpha: Somma di frazioni
Notare l'uso dell'operatore Together che verrà descritto in seguito.
Progressione aritmetica di 10 termini con primo termine 1/2 e ragione 1/3. WolframAlpha: Progressione aritmetica
Progressione geometrica di 10 termini con primo termine 1/2 e ragione 1/3. WolframAlpha: Progressione geometrica
Anche il calcolo di espressioni contenenti irrazionali è sempre matematicamente esatto.
Ad esempio, calcolando l'espressione trigonometrica.
Cos[Pi/3]+Sin[Pi/3]
Si ottiene
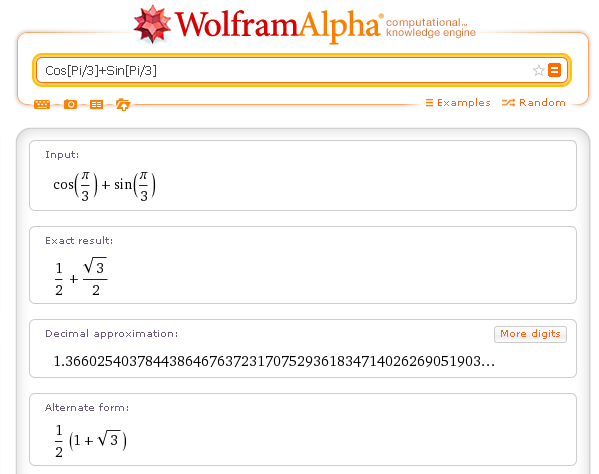
Come si vede, gli irrazionali sono preferibilmente indicati simbolicamente con radicali, logaritmi o in generale come valori di funzioni algebriche o trascendenti, dirette o inverse, di argomenti razionali.
| Mathematica | risultato | esempio |
|---|---|---|
| Pi | pi greca | Pi/2; Sin[2Pi/3] |
| E | la base naturale (numero di Nepero) | E^x; Log[Sqrt[E]] |
| GoldenRatio | il numero | 1/GoldenRatio |
| Degree | un grado sessagesimale espresso in radianti | Sin[60 Degree] |
| I | l'unità immaginaria | (1+I)^2; Abs[3+4I] |
| Infinity | ∞ | Limit[(x+1)/x,x->Infinity] |
| Mathematica | risultato | esempio |
|---|---|---|
| Abs[z] | valore assoluto o modulo di complesso | Abs[3+4I] |
| Sqrt[z] | radice quadrata | Sqrt[2]; Sqrt[1+I] |
| Exp[z] | esponenziale naturale (anche E^z) | Exp[2]; E^2 |
| Log[z] | logaritmo naturale | Log[E^2] |
| Log[b,z] | logaritmo in base b | Log[2,8] |
| Sin[z] | seno circolare | Sin[Pi/6] |
| Cos[z] | coseno circolare | Cos[Pi/6] |
| Tan[z] | tangente circolare | Tan[Pi/4] |
| ArcSin[z] | arcoseno circolare | ArcSin[1/2] |
| ArcCos[z] | arcocoseno circolare | ArcCos[1/2] |
| ArcTan[z] | arcotangente circolare | ArcTan[Sqrt[3]] |
| Sinh[z] | seno iperbolico | Sinh[1] |
| Cosh[z] | coseno iperbolico | Cosh[1] |
| Tanh[z] | tangente iperbolica | Tanh[1] |
| ArcSinh[z] | arcoseno iperbolico | ArcSinh[1] |
| ArcCosh[z] | arcocoseno iperbolico | ArcCosh[1/2] |
| ArcTanh[z] | arcotangente iperbolica | ArcTanh[2] |
Esempio.
(1+I)^2
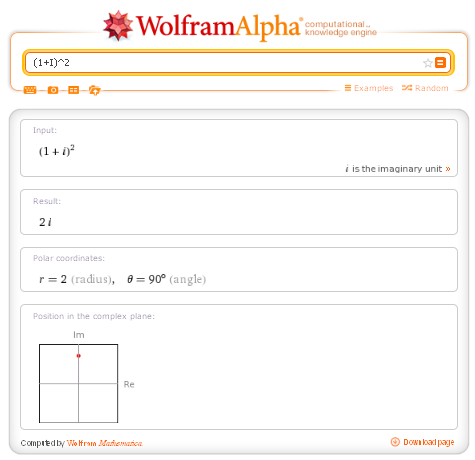
Gli argomenti delle funzioni trigonometriche si intendono sempre in radianti.
Nel caso li si voglia esprimere in gradi sessagesimali vanno moltiplicati per la costante predefinita Degree.
Altri esempi.