| Mathematica | risultato | esempio |
|---|---|---|
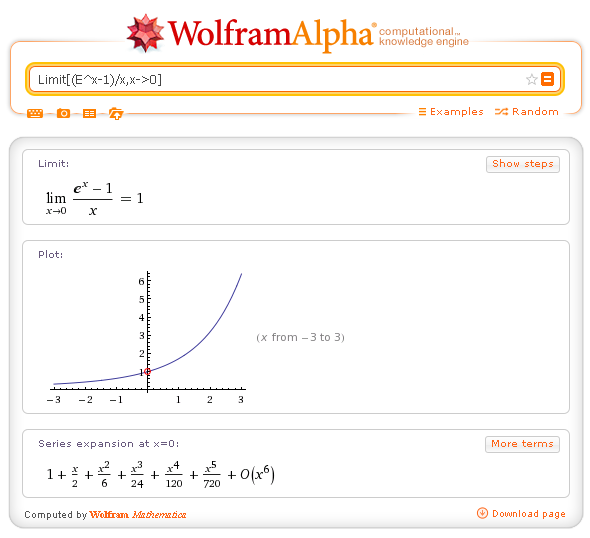
| Limit[f[x],x->x0] | calcola il limite per x→x0 | Limit[(E^x-1)/x,x->0] |
| Limit[f[x],x->Infinity] | calcola il limite per x→∞ | Limit[1/x,x->Infinity] |
| Dt[f[x],x] | calcola la derivata prima di f(x) rispetto a x | Dt[Sin[2x]^2,x] |
| Dt[f[x]] | calcola il differenziale di f(x) | Dt[Sin[2x]^2] |
| Dt[f[x],{x,n}] | calcola la derivata n-esima di f(x) rispetto a x | Dt[Sin[2x]^2,{x,2}] |
| D[f[x,y],x] | calcola la derivata parziale di f(x,y) rispetto a x | D[Sin[x y],x] |
| D[f[x,y],{x,n}] | calcola la derivata parziale n-esima di f(x,y) rispetto a x | D[Sin[x y],{x,2}] |
| Integrate[f[x],x] | calcola l'integrale indefinito di f(x) in dx | Integrate[Log[x],x] |
| Integrate[f[x],{x,xmin,xmax}] | calcola l'integrale definito di f(x) in dx nell'intervallo [xmin,xmax] | Integrate[Log[x],{x,1,E}] |
| DSolve[equazione,y,x] | risolve l'equazione differenziale sulla funzione y della variabile x | DSolve[y'[x]==y,y,x] |
| Series[f[x],{x,0,n}] | calcola n termini dello sviluppo in serie di Maclaurin di f(x) | Series[Exp[x],{x,0,10}] |
| Series[f[x],{x,x0,n}] | calcola n termini dello sviluppo in serie di Taylor di f(x) in un intorno di x0 | Series[Log[x],{x,1,10}] |
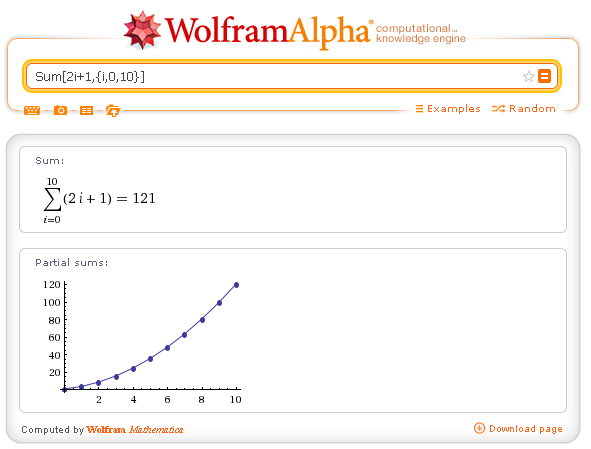
| Sum[f[i],{i,imin,imax}] | calcola la somma degli addendi f[i] con i da imin a imax incrementando i di 1 ad ogni passo | Sum[2i+1,{i,0,10}] |
| Sum[f[i],{i,imin,imax,inc}] | calcola la somma degli addendi f[i] con i da imin a imax incrementando i di inc ad ogni passo | Sum[2i+1,{i,0,10}] |
Esempi.
Limite: Limit[(E^x-1)/x,x->0]

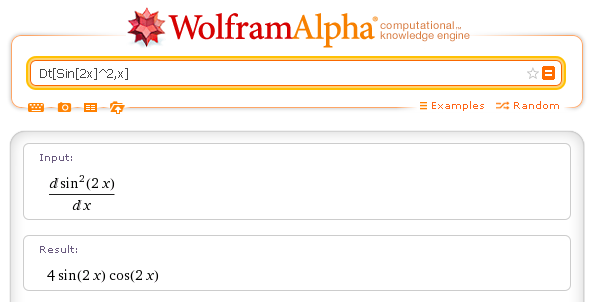
Derivata: Dt[Sin[2x]^2,x]
Integrale indefinito: Integrate[Log[x],x]
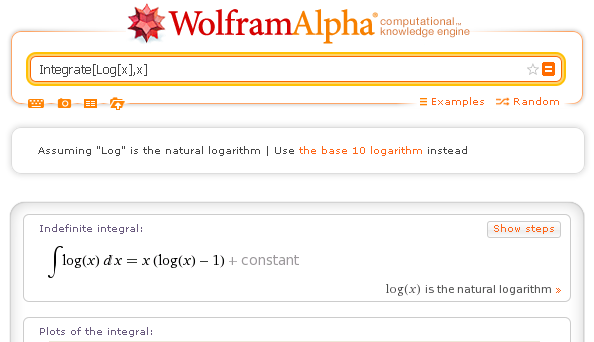
Cliccando il bottone Show steps si ottiene la dimostrazione.
Per il calcolo di un integrale indefinito è direttamente disponibile in linea anche Wolfram Integrator
Integrale definito: Integrate[Log[x],{x,1,E}]
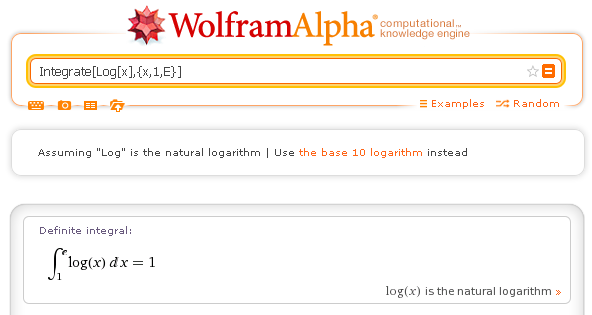
Per il calcolo di un integrale definito è direttamente disponibile in linea anche
Definite Integral Calculator
che può essere anche trasferito in una propria pagina Html semplicemente ricopiando lo script fornito, come si fa
qui di seguito
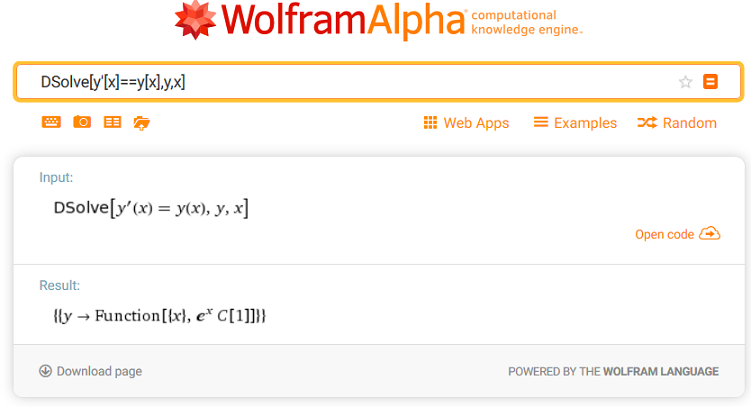
Equazione differenziale: DSolve[y'[x]==y[x],y,x]
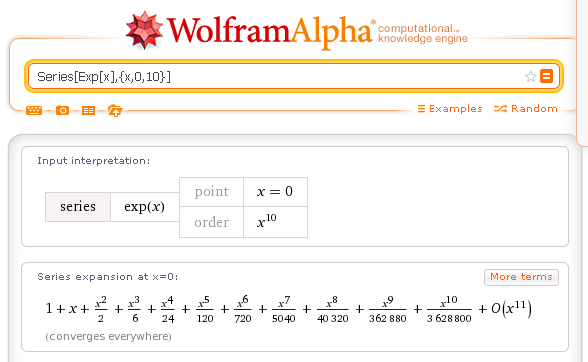
Sviluppo in serie di Maclaurin: Series[Exp[x],{x,0,10}]
Somma dei primi 11 numeri dispari: Sum[2i+1,{i,0,10}]