SuperCalcolatrice è implementata in Javascript, quindi è utilizzabile solo se il browser in uso permette Javascript.
SuperCalcolatrice presenta tabelle e grafici in finestre popup, quindi per il suo completo funzionamento il browser le deve consentire.
Se il browser non consente la visualizzazione dei frames interni, potete aprire direttamente la pagina dell'applicazione.
SuperCalcolatrice è destinata ad uso didattico, non professionale; non si assumono responsabilità per eventuali imprecisioni o errori.
Prestazioni, istruzioni, esempi.
SuperCalcolatrice, a differenza di un'ordinaria calcolatrice,
Il calcolo sugli interi e sui razionali rappresentati con frazioni è sempre esatto.
Il calcolo sugli interi utilizza una libreria di L. Baird.
I risultati dei calcoli sui razionali sono rappresentati da frazioni.
I numeri razionali possono essere immessi anche come decimali periodici.
In questo caso il periodo va posto tra parentesi quadre.
Esempio: 1.2[34].
Se il calcolo coinvolge numeri reali, i risultati possono essere approssimati al numero predeterminato di decimali
impostato nel campo decimali (di default 6).
Se si imposta questo valore ad un numero molto alto, i tempi di calcolo possono diventare intollerabili.
Nel campo tempo può essere impostato in secondi il tempo massimo di attesa (di default 1).
Il separatore decimale per i numeri reali è il punto.
I numeri in formato sessagesimale in uso per misure angolari sono espressi da tre gruppi di cifre separate dai simboli °, ', " per gradi, primi e secondi.
Le eventuali espressioni dei gradi, primi e secondi in input possono essere numeri razionali; in output l'espressione viene normalizzata
in modo che i gradi sono espressi da numeri naturali, i primi da numeri naturali < 60 e i secondo da razionali < 60.
Esempio: 12°15'18"+34°56'55.34571"; Sin[30°]; a=15.45°; b=12.18°78'; a+b
I reali possono essere immessi anche in forma esponenziale. In questo caso la lettera E deve essere maiuscola.
Esempio: 1.234E5.
L'unità immaginaria, in input e output, è indicata dal carattere maiuscolo I. Un numero complesso può essere immesso in modo simile ai seguenti:
2I; 1+3I; 5-12I;1/2I; 1/2+3/4I; 1.2[3]I; 1.2-3.4[56]I;I valori booleani sono rappresentati con i caratteri V e F, obbligatoriamente maiuscoli. Con l'uso degli appropriati operatori descritti in seguito si possono eseguire calcoli booleani. Esempi:
(V&&F)==FF->V;Vettori e matrici vanno scritti in linea usando le parentesi graffa opportunamente annidate.
Il selettore costanti permette di inviare nel campo di input i valori delle più comuni costanti matematiche e fisiche.
Si possono memorizzare altre costanti numeriche, vettoriali o matriciali assegnando il loro valore ad opportuni identificatori.
Il selettore operatori permette di inviare nel campo di input i nomi dei più comuni operatori matematici.
Per ottenere documentazione sull'uso degli operatori disponibili, usare il punto interrogativo ? seguito dal nome dell'operatore. Il formato maiuscolo o minuscolo dei caratteri è ininfluente.
Es. ?fibonacci.
Input e output
Nel campo input possono essere impostate espressioni
da calcolare immediatamente, scrivendole in linea con le usuali convenzioni per le
operazioni e attivando il bottone ![]() .
.
È possibile scrivere in input più istruzioni separandole con un punto e virgola (;).
Esempio: 100!; FP[100!].
Esempio: f[x]:=x^2-1; Grafico[x,f[x],-2,2].
Esempio: c=Circ[{0,0},1]; Disegno[c].
Per impostare un nuovo calcolo si può cliccare sul bottone nuovo input
oppure semplicemente cliccare con il mouse sul campo di input.
Nel campo di input si possono dichiarare funzioni da usare
in calcoli successivi e si può assegnare un valore ad una costante.
In questi due casi l'attivazione del bottone calcolo non produce un
risultato esplicito, ma solo la memorizzazione della funzione o della costante.
Ad ogni attivazione del bottone calcolo si ottiene nel
campo output la ripetizione dell'espressione immessa seguita dal risultato
prodotto. Input e output sono numerati in modo da poterli richiamare con i
comandi In e Out.
I risultati ottenuti in output possono essere salvati in un file locale selezionando il testo, attivando la funzione copia (ctrl c), aprendo un editor di testo (ad es. Notepad),
incollandoli (ctrl v) e salvando il file così generato nella collocazione opportuna.
Tutto il contenuto dell'output può essere salvato in un file locale in formato *.txt scrivendone il nome nella sezione salva foglio e cliccando il bottone salva.
Il contenuto di un foglio salvato può essere riimmesso nel campo output selezionando nella sezione carica foglio un file di testo precedentemente salvato e cliccando
sul bottone carica. In questo caso comunque il foglio non viene calcolato. Per ricalcolarne alcune espressioni può
essere utile aprire un foglio con un editor di testo, selezionare le espressioni da ricalcolare, copiarle e incollarle nella sezione input.
Dato che immagini e tabelle sono prodotte in pagine autonome, è necessario che il browser in uso consenta l'apertura di popup.
Le pagine generate nei popup possono essere salvate con la procedura standard salva pagina con nome.
Nelle pagine con i grafici, in Chrome e in Firefox, il grafico può essere salvato come immagine in formato png cliccando su di esso e indicando nome e collocazione dell'immagine.
Le espressioni immediate e le dichiarazioni di costante e di funzione possono contenere i seguenti segni di operazione:
| segno | operazione |
|---|---|
| + | addizione |
| - | sottrazione |
| * | moltiplicazione (anche spazio vuoto) |
| / | divisione reale |
| ^ | potenza |
| ! | fattoriale |
| !! | doppio fattoriale |
I seguenti segni di operazione agiscono solo su operandi naturali producendo risultati naturali. Gli operatori logici eseguono calcoli bitwise.
| segno | operazione |
|---|---|
| : | divisione tra interi |
| % | resto nella divisione tra interi |
| && | and |
| || | or |
| ## | xor |
| !| | nor |
| !& | nand |
| #| | xnor |
| -> | implicazione materiale |
I seguenti segni di operazione agiscono su operandi logici (booleani).
| segno | operazione |
|---|---|
| - | non (negazione) |
| && | and |
| || | or |
| ## | xor |
| !| | nor |
| !& | nand |
| #| | xnor |
| -> | implicazione materiale |
Alcune operazioni aritmetiche binarie possono essere indicate il forma prefissa, costituita dal nome di un operatore seguito da una coppia di parentesi quadre contenenti i due operandi.
| operatore | operazione | esempio |
|---|---|---|
| Piu[x,y] | somma | Piu[4,3] |
| Meno[x,y] | sottrazione | Meno[4,3] |
| Per[x,y] | prodotto | Per[4,3] |
| Diviso[x,y] | divisione | Diviso[4,3] |
| Potenza[x,y] | potenza | Potenza[4,3] |
| Quoz[x,y] | quoziente tra interi | Quoz[24,5] |
| Resto[x,y] | resto di divisione tra interi | Resto[24,5] |
Anche alcune operazioni logiche o bitwise binarie possono essere indicate il forma prefissa, costituita dal nome di un operatore seguito da una coppia di parentesi quadre contenenti i due operandi.
| operatore | operazione | esempio |
|---|---|---|
| Or[x,y] | disgiunzione inclusiva | Or[V,F]; Or[2,3] |
| And[x,y] | congiunzione | And[V,f]; And[4,3] |
| Xor[x,y] | disgiunzione esclusiva | Xor[V,F]; Xor[4,3] |
| Nor[x,y] | not Or | Nor[V,F]; Nor[4,3] |
| Nand[x,y] | not And | Nand[V,F]; Nand[4,3] |
| Xnor[x,y] | Nor esclusivo | Xnor[V,F]; Xnor[4,3] |
| Impl[x,y] | implicazione materiale | Impl[V,F]; Impl[4,3] |
L'ordine di esecuzione dei calcoli in un'espressione è indicato dalle parentesi tonde eventualmente annidate.
Nelle espressioni si possono usare le seguenti costanti predefinite (maiuscole e minuscole sono obbligatorie).
(Per le costanti fisiche la precisione è limitata al loro valore sperimentale.)
| costante | nome |
|---|---|
| P | pi greca |
| E | base naturale |
| PHI | numero aureo |
| I | unità immaginaria |
| V | verità logica |
| F | falsità logica |
| GAMMA | Gamma di Eulero-Mascheroni |
| G | costante di Gravitazione Universale |
| PLANCK | costante di Planck |
| C | velocità della luce nel vuoto |
| AVOG | numero di Avogadro |
| R | costante dei gas perfetti |
| BOLTZ | costante di Boltzmann |
| ELM | massa a riposo dell'elettrone |
| ELC | carica dell'elettrone |
| PRM | massa a riposo del protone |
| PRC | carica del protone |
| EPS0 | permittività elettrica del vuoto |
| MU0 | permeabilità magnetica del vuoto |
| RYDB | costante di Rydberg |
| BOHR | raggio di Bohr |
| COMPTON | lunghezza d'onda di Compton |
| STEFAN | costante di Stefan-Boltzmann |
| SG | accelerazione di gravità terrestre standard |
| ATM | Atmosfera in Pascal |
Nelle espressioni si possono usare le seguenti funzioni che richiedono un solo argomento reale o complesso (eccezionalmente 2 per radici, logaritmi e potenze). Se l'argomento è indicato con x, la funzione ammette solo variabile reale; se l'argomento è indicato con z, la funzione ammette variabile reale o complessa. Si possono ottenere tabulazioni e grafici solo delle funzioni reali di variabile reale.
| funzione | nome | esempio |
|---|---|---|
| Int[x] | parte intera | Int[P] |
| Frac[x] | parte decimale | Frac[P] |
| Abs[z] | val. assoluto | Abs[1+I] |
| Rec[z] | reciproco (inverso moltiplicativo) | Rec[1+I] |
| Arg[z] | argomento di complesso | Arg[3+4I] |
| Real[z] | parte reale di complesso | Real[3+4I] |
| Im[z] | parte immaginaria di complesso | Im[3+4I] |
| Sqr[z] | quadrato | Sqr[3]; Sqr[1+I] |
| Cube[z] | cubo | Cube[3]; Cube[1+I] |
| Sqrt[z] | radice quadrata | Sqrt[P]; Sqrt[1+I] |
| Cubert[x] | radice cubica | Cubert[P]; Cubert[1+I] |
| Radice[n,z] | radice n-esima (n naturale ≥ 2) | Radice[3,8]; Radice[4,P]; Radice[5,I] |
| Radici[n,z] | radici n-esime (n naturale ≥ 2) | Radici[3,8]; Radici[4,P]; Radici[5,I] |
| Fact[z] | fattoriale | Fact[100]; Fact[P]; Fact[1+I] |
| Sin[z] | seno circolare | Sin[P/2]; Sin[ArcSin[2]] |
| Cos[z] | coseno circolare | Cos[P/4]; Cos[ArcCos[2]] |
| Tan[z] | tangente circolare | Tan[P/4]; Tan[1+I] |
| Sec[z] | secante circolare | Sec[P/3]; Sec[1+I] |
| Cosec[z] | cosecante circolare | Cosec[P/2]; Sec[1+I] |
| Cotan[z] | cotangente circolare | Cotan[P/4]; Cotan[1+I] |
| ArcSin[z] | arcoseno circolare | ArcSin[1/2]; ArcSin[1+I] |
| ArcCos[z] | arcocoseno circolare | ArcCos[1/2]; ArcCos[1+I] |
| ArcTan[z] | arcotangente circolare | ArcTan[Sqrt[3]]; ArcTan[1+I] |
| Exp[z] | esponenziale naturale | Exp[-2]; Exp[I] |
| Ln[z] | logaritmo naturale | Ln[Sqr[E]]; Ln[1+I] |
| Log[β,z] | logaritmo in base β | Log[2,16]; Log[I,Cube[I]] |
| Sinh[z] | seno iperbolico | Sinh[Ln[2]]; Sinh[1+I] |
| Cosh[z] | coseno iperbolico | Cosh[Ln[2]]; Cosh[1+I] |
| Tanh[z] | tangente iperbolica | Tanh[Ln[2]]; Tanh[1+I] |
| Sech[z] | secante iperbolica | Sech[1]; Sech[1+I] |
| Cosech[z] | cosecante iperbolica | Cosech[1]; Cosech[1+I] |
| Cotanh[z] | cotangente iperbolica | Cotanh[P/4]; Cotanh[1+I] |
| ArcSinh[z] | arcoseno iperbolico | ArcSinh[1]; ArcSinh[1+I] |
| ArcCosh[z] | arcocoseno iperbolico | ArcCosh[2]; ArcCosh[1+I] |
| ArcTanh[z] | arcotangente iperbolica | ArcTanh[1]; ArcTanh[1+I] |
| Gamma[z] | gamma di Eulero | Gamma[11]==10!; Gamma[1+I] |
| Zeta[x] | funzione Zeta di Riemann | Zeta[-2] |
| EllipticK[x] | integrale ellittico completo di prima specie | EllipticK[1/2] |
| EllipticE[x] | integrale ellittico completo di seconda specie | EllipticE[1/2] |
| Random[x] | n. casuale positivo < x, intero o reale a seconda del tipo di x | Random[10]; Random[10.] |
| Erf[x] | funzione degli errori | Erf[1] |
| Gauss[x] | Gaussiana normalizzata (media 0) | Gauss[1] |
Queste funzioni possono essere graficate o tabulate direttamente negli intervalli in cui producono valori reali.
Esempio:
Grafico[x,Sin[x],0,2P] Grafico[x,Erf[x],-2,2,0.1] Tabella[x,Sqrt[x],0,4] Coordinate[x,Cosh[x],-1,1,0.1]
Sono disponibili anche le seguenti funzioni con argomenti reali.
| funzione | nome | esempio |
|---|---|---|
| DBinomiale[x,n,k] | distribuzione binomiale con probabilità x (0 ≤ x ≤ 1) | DBinomiale[0.3,10,4] |
| Poisson[λ,k] | probabilità che un evento si verifichi k volte in una distribuzione poissoniana con media λ | Poisson[0.5,2] |
| LegendreP[n,x] | polinomio di Legendre di prima specie | LegendreP[3,x] |
| LegendreQ[n,x] | polinomio di Legendre di seconda specie | LegendreQ[3,x] |
| ChebyshevT[n,x] | polinomi di Chebyshev di prima specie | ChebyshevT[3,x] |
| ChebyshevU[n,x] | polinomi di Chebyshev di seconda specie | ChebyshevU[3,x] |
| GaussS[x,σ] | Gaussiana con dev. standard σ e media 0 | GaussS[1,1/2] |
| GaussSM[x,σ,μ] | Gaussiana con dev. standard σ e media μ | GaussSM[2,1,0.5] |
Queste funzioni non sono tabulabili o graficabili direttamente. Per ottenere il loro grafico è necessario dichiarare una funzione di una sola variabile reale in cui esse compaiano a secondo membro della dichiarazione.
Esempio:
db[n]:=DBinomiale[0.5,10,n]; Tabella[n,db[n],0,10,1]
I seguenti operatori agiscono su un numero reale.
| operatore | effetto | esempio |
|---|---|---|
| FrAppr[x] | produce la frazione che meglio approssima il valore assoluto di x con la precisione vigente. | FrAppr[P]; FrAppr[Sqrt[2]] |
| AContinua[x] | produce la sequenza di numeri naturali corrispondenti allo sviluppo del reale del valore assoluto di x in funzione continua con la precisione vigente. | AContinua[PHI] |
| RadDeg[x] | da radianti a gradi decimali | RadDeg[P/3] |
| RadSec[x] | da radianti a secondi | RadSec[P/3] |
| RadDms[x] | da radianti a gradi sessagesimali | RadDms[P/3] |
| DegRad[x] | da gradi decimali a radianti | DegRad[60] |
| DegDms[x] | da gradi decimali a gradi sessagesimali | DegDms[1.5] |
| DegSec[x] | da gradi decimali a secondi | DegSec[1] |
| SecRad[x] | da secondi a radianti | SecRad[100000] |
| SecDeg[x] | da secondi a gradi decimali | SecDeg[100000] |
| SecDms[x] | da secondi a gradi sessagesimali | SecDms[100000] |
I seguenti operatori agiscono su argomenti sessagesimali.
| operatore | effetto | esempio |
|---|---|---|
| DmsRad[x] | da gradi sessagesimali a radianti | DmsRad[45°12'34"] |
| DmsDeg[x] | da gradi sessagesimali a gradi decimali | DmsDeg[45°12'34"] |
| DmsSec[x] | da gradi sessagesimali a secondi | DmsSec[45°12'34"] |
Per i calcoli statistici si possono usare seguenti operatori che agiscono su su liste di numeri reali o su coppie di numeri reali.
| operatore | effetto | esempio |
|---|---|---|
| Media[lista] | media aritmetica | Media[P,E,Sqrt[2]] |
| SSigma[lista] | deviazione standard campionaria | SSigma[P,E,Sqrt[2]] |
| PSigma[lista] | deviazione standard della popolazione | PSigma[P,E,Sqrt[2]] |
Inoltre si possono usare i seguenti operatori che agiscono su liste di coppie di numeri reali.
| operatore | effetto | esempio |
|---|---|---|
| Pcc[lista di coppie] | coefficiente di correlazione lineare di Pearson | Pcc[{1,2},{2,3},{3,4},{4,5}] |
| Ols[lista di coppie] | (Ordinary least squares): retta di regressione lineare | Ols[{1,2},{2,3},{3,4},{4,5}] |
| Qls[lista di coppie] | (Quadratic least squares): parabola di regressione | Qls[{-1,2},{0,1},{1,2}] |
| Pls[g,lista di coppie] | (Polynomial least squares): polinomio di grado g di regressione | Pls[3,{{-2,0},{-1,-1},{0,0},{1,1},{2,0}}] |
La lista può essere rappresentata da una costante precedentemente dichiarata. Ad esempio:
dati = 12,14,13,15,11,12,12,14; Media[dati]
dati2 = {1,2},{2,3},{3,4},{4,5}; Pcc[dati2]
I seguenti operatori agiscono su argomenti razionali.
| operatore | effetto | esempio |
|---|---|---|
| Num[f] | numeratore della frazione ridotta ai minimi termini | Num[Bernoulli[10]] |
| Den[f] | denominatore della frazione ridotta ai minimi termini | Den[Bernoulli[10]] |
| N[f] | da razionale a decimale | N[2/3]; N[1.2[3]] |
| Egizie[f,maxl,maxn] | sviluppa una frazione in somme di frazioni egizie (o egiziane), cioè di numeratore 1; maxl è il massimo n. di addendi; maxn è il massimo numero di sviluppi | Egizie[3/7,5,5] |
| AContinua[f] | produce la sequenza di numeri naturali corrispondenti allo sviluppo del valore assoluto della frazione f in funzione continua. | AContinua[79/122] |
| DaContinua[a0,a1,a2,...an] | restituisce la frazione dati i coefficienti del suo sviluppo in funzione continua. | DaContinua[0,1,1,1,5,7] |
I seguenti operatori agiscono su uno o più numeri naturali.
| operatore | effetto | esempio |
|---|---|---|
| Mcd[lista] | massimo comun divisore | Mcd[123456,234567,345678] |
| Mcm[lista] | minimo comune multiplo | Mcm[123,234,345] |
| Primo[n] | vero o falso se l'argomento è primo o no; valori molto grandi di n possono implicare tempi di calcolo impraticabili. | Primo[1234567] |
| Scomposizione[n] | scomposizione in fattori primi di un n. naturale; valori molto grandi di n possono implicare tempi di calcolo impraticabili. | Scomposizione[1234567] |
| NPrimo[n] | ennesimo numero primo | NPrimo[12] |
| Partizione[n] | calcolo della funzione di partizione di un numero naturale | Partizione[100] |
| Base[n,b] | cambio di base nella notazione di un naturale in base dieci | Base[1234,16] |
| DecHex[n] | rappresentazione esadecimale di un naturale in base dieci | DecHex[1234567890] |
| HexDec[n] | rappresentazione decimale di un naturale esadecimale | HexDec[ABCDEF] |
| HexBin[n] | rappresentazione in base due di un naturale esadecimale | HexBin[ABCDEF] |
| DecBin[n] | rappresentazione in base due di un naturale in base dieci | DecBin[1234567890] |
| BinDec[n] | rappresentazione decimale di un naturale in base due | BinDec[10000101010100000111] |
| BinHex[n] | rappresentazione esadecimale di un naturale in base due | BinHex[10000101010100000111] |
| Fibonacci[n] | ennesimo numero della successione di Fibonacci | Fibonacci[1234]; Tabella[n,Fibonacci[n],0,100,1] |
| Padovan[n] | ennesimo numero della successione di Padovan | Padovan[1234] |
| Perrin[n] | ennesimo numero della successione di Perrin | Perrin[1234] |
| Bernoulli[n] | ennesimo numero di Bernoulli | Bernoulli[14] |
| Euler[n] | ennesimo numero di Eulero | Euler[14] |
| Bell[n] | ennesimo numero di Bell | Bell[12]; Tabella[n,Bell[n],0,50,1] |
| DFact[n] | doppio fattoriale | DFact[14] |
| Terne[min,max] | terne pitagoriche formate da numeri naturali compresi tra min e imax | Terne[3,100] |
| Collatz[n] | sequenza di Collatz | Collatz[27] |
| Binomiale[n,k] | coefficiente binomiale | Binomiale[100,37] |
| StirlingS[n,k] | numero di Stirling di seconda specie | StirlingS[100,37] |
Binomiale opera anche su coppie di reali o complessi.
I seguenti operatori agiscono su una o più funzioni reali di variabile reale e sulla loro rappresentazione grafica. Il numero di punti da calcolare e i valori massimi e minimi graficabili vanno impostati negli appositi campi prima di attivare l'operatore.
| operatore | effetto | esempio |
|---|---|---|
| Derivata[x,f[x],x0] | calcolo approssimato della derivata della funzione in un punto del suo dominio | Derivata[x,Sin[x],0] |
| Integrale[x,f[x],x1,x2] | calcolo approssimato dell'integrale della funzione in un intervallo del suo dominio | Integrale[x,Sin[x],0,P/2] |
| Tabella[x,f[x],x1,x2] | produzione della tabella di una funzione in un intervallo dato usando un numero fisso di valori dell'argomento | Tabella[x,Sin[x],0,2P] |
| Tabella[x,f[x],x1,x2,dx] | produzione della tabella di una funzione in un intervallo dato con incremento prefissato dell'argomento | Tabella[n,NPrimo[n],0,100,1] |
| Coordinate[x,f[x],x1,x2] | produzione della lista delle coppie {x,y} di una funzione in un intervallo dato usando un numero fisso di valori dell'argomento | Coordinate[x,Sin[x],0,2P] |
| Coordinate[x,f[x],x1,x2,dx] | produzione della lista delle coppie {x,y} di una funzione in un intervallo dato con incremento prefissato dell'argomento | Coordinate[x,Sin[x],0,2P,P/6] |
| Valori[x,f[x],x1,x2] | produzione della lista dei valori y di una funzione in un intervallo dato usando un numero fisso di valori dell'argomento | Valori[x,Sin[x],0,P] |
| Valori[x,f[x],x1,x2,dx] | produzione della lista dei valori y di una funzione in un intervallo dato con incremento prefissato dell'argomento | Valori[n,Fibonacci[n],0,100,1] |
| Zeri[x,f[x],x1,x2] | approssimazione degli zeri di una funzione in un intervallo dato | Zeri[x,Sin[2x],0,2P] |
| Studio[x,f[x],x1,x2] | studio dei punti rilevanti del grafico di una funzione in un intervallo dato con produzione del grafico | Studio[x,Sin[x],0,2P] |
Istogramma permette di produrre grafici di funzioni di variabile discreta (anche non numerica)
con grafico a canne d'organo. Esempi:
f[k] := Binomiale[10,k]; Istogramma["coefficienti binomiali",Coordinate[k,f[k],0,10,1]]
lista_temperature = ("Roma",20),("Milano",15),("Napoli",22); Istogramma["temperature",lista_temperature]
I seguenti operatori permettono di rilevare alcune proprietà dei vettori reali o complessi.
| operatore | effetto | esempio |
|---|---|---|
| Modulo[v] | calcola il modulo di un vettore | Modulo[{1,2,3,4}] |
| Anomalia[v] | calcola l'anomalia (o angolo polare) di un vettore reale bidimensionale | Anomalia[{1/2,Sqrt[3]/2}] |
| Versore[v] | calcola il vettore unitario allineato con il vettore dato | Versore[{1,Sqrt[3]}] |
I seguenti operatori permettono di produrre e rappresentare grafici di funzioni reali di variabile reale e alcune figure geometriche piane.
| operatore | effetto | esempio |
|---|---|---|
| RangeX[x1,x2] | valori minimo e massimo delle ascisse dei punti graficabili: di default [-10,10] | RangeX[-20,20] |
| RangeY[y1,y2] | valori minimo e massimo delle ordinate dei punti graficabili: di default [-10,10] | RangeY[-20,20] |
| Grafico[x,f[x],x1,x2] | disegno del grafico di una funzione in un intervallo usando un numero fisso di valori dell'argomento ugualmente distanziati | Grafico[x,Sqr[Sin[x]],0,2P] |
| Grafico[x,f[x],x1,x2,dx] | disegno del grafico di una funzione in un intervallo con incremento prefissato dell'argomento | Grafico[x,x^2-1,-2,2,0.1] |
| Grafico[x,{f[x],g[x]},x1,x2] | disegno del grafico di più funzioni in un intervallo dato usando un numero fisso di valori dell'argomento | Grafico[x,{Sin[x],Cos[x]},0,2P] |
| Grafico[x,{f[x],g[x]},x1,x2,dx] | disegno del grafico di più funzioni in un intervallo dato con incremento prefissato dell'argomento | Grafico[x,{Sin[x],Cos[x]},0,2P,0.1] |
| Istogramma[titolo,lista] | disegno dell'istogramma con titolo di una lista | t = {{"Roma",20},{"Milano",15},{"Napoli",22}};Istogramma["temperature",t] |
| Circ[{xc,yc},r] | definisce una circonferenza dati centro e raggio | c=Circ[{0,0},1] |
| Ellisse[{xc,yc},a,b] | definisce un'ellisse dati centro e semiassi | el=Ellisse[{0,0},3,1] |
| PoliV[{xc,yc},r,n] | definisce un poligono regolare dati centro, raggio circoscritto e numero di lati | etta=PoliV[{0,0},1,7] |
| Disegno[oggetto grafico] | disegna uno degli oggetti generati dagli operatori precedenti | c=Circ[{0,0},1]; Disegno[c] |
| Disegno[lista di oggetti grafici] | disegna contemporaneamente più oggetti generati dagli operatori precedenti | c1=Circ[{0,0},1]; c2=Circ[{0,0},2]; Disegno[c1,c2] |
| Traslazione[oggetto grafico,(x,y)] | trasla gli oggetti grafici generati dagli operatori precedenti | q=PoliV[{0,0},1,4]; tq=Traslazione[q,{-1,1}]; Disegno[tq] |
| Rotazione[oggetto grafico,α] | ruota gli oggetti grafici generati dagli operatori precedenti | q=PoliV[{0,0},1,4]; rq=Rotazione[q,30°]; Disegno[rq] |
I seguenti operatori agiscono su matrici quadrate.
| operatore | effetto | esempio |
|---|---|---|
| Det[m] | calcolo del determinante di una matrice quadrata | Det[{{1,2},{0,1}}] |
| Trasposta[m] | calcola la matrice trasposta | Trasposta[{{1,2},{0,1}}] |
| Inversa[m] | calcola la matrice inversa di una matrice quadrata | Inversa[{{1,2},{0,1}}] |
| Coniugata[m] | calcola la matrice coniugata | Coniugata[{{1,2},{0,1}}] |
| Aggiunta[m] | calcola la matrice aggiunta | Aggiunta[{{1,2},{0,1}}] |
| AutoValori[m] | calcolo degli autovalori | AutoValori[{{1,2},{2,3}}] |
| AutoVettori[m] | calcola degli autovettori | AutoVettori[{{1,2},{2,3}}] |
| AutoSistema[m] | calcolo di autovalori e autovettori | AutoSistema[{{1,2},{2,3}}] |
| SolLineare[m,v] | data una matrice m e un vettore v, risolve un sistema lineare | SolLineare[{{1,2},{0,1}},{3,4}] |
Con i normali segni di operazione si possono eseguire somme, sottrazioni, prodotti, divisioni e potenze ad esponente intero (positivo o negativo) su matrici.
Esempio.
m1={1,2,3}{2,-1,0}{-2,1,3}m1^2m2={5,2,1}{1,-1,3}{-1/2,0,1}m1*m2
I seguenti operatori modificano il contenuto di liste di oggetti.
| operatore | effetto | esempio |
|---|---|---|
| Aggiungere[l,o] | Data la lista l e un oggetto o, colloca l'oggetto in coda alla lista | Aggiungere[{1,2,3},4] |
| Inserire[l,o,ix] | Data la lista l, un oggetto o e una posizione ix, colloca l'oggetto in posizione ix all'interno di l | Inserire[{1,2,4,5},3,2] |
| Eliminare[l,ix] | Data la lista l e una posizione ix, elimina da l l'oggetto in posizione ix | Eliminare[{1,2,3,4,5},2] |
| Sostituire[l,o,ix] | Data la lista l, un oggetto o e una posizione ix, elimina da l l'oggetto in posizione ix e lo sostituisce con o | Sostituire[{1,2,3,4,5},33,2] |
| OrdinareA[l] | Data la lista l contenente valori numerici o stringhe, la ordina in senso ascendente cioè dal minore al maggiore | OrdinareA[1,-4,P,R,11/3,2e-1,2^5] |
| OrdinareD[l] | Data la lista l contenente valori numerici o stringhe, la ordina in senso discendente cioè dal maggiore al minore | OrdinareD[1,-4,P,R,11/3,2e-1,2^5] |
| Concatenare[l1,l2] | Data le liste di stringhe l1 e l2, ne forma una sola accodando gli elementi di l2 a quelli di l1. | l1 = {"Milano","Roma","Napoli"}; l2 = {"Torino","Palermo"}; Concatenare[l1,l2] |
| Unire[l1,l2] | Data le liste di stringhe l1 e l2, ne forma una sola accodando agli elementi di l1 gli elementi di l2 non presenti in l1. | l1 = {"Milano","Roma","Napoli"}; l2 = {"Milano","Torino","Palermo"}; Unire[l1,l2] |
| Intersecare[l1,l2] | Data le liste di stringhe l1 e l2, ne forma una sola composta dagli elementi comuni a l1 e l2. | l1 = {"Milano","Roma","Napoli"}; l2 = {"Milano","Torino","Palermo"}; Intersecare[l1,l2] |
| Frequenze[l] | Data la lista l contenente valori numerici non complessi, raggruppa i valori presenti in ordine crescente esprimendo quante volte compaiono nella lista. | r[x]:=Random[10]; Frequenze[Valori[x,r[x],1,100,1]] |
I seguenti operatori eseguono calcoli di interesse finanziario.
| operatore | effetto | esempio |
|---|---|---|
| Percent[x,i] | dato un numero e un percento, calcola la percentuale del numero | Percent[123456.78,3.45] |
| RataMutuo[m,i,n,k] | dati mutuo m, interesse nominale percentuale annuo i, durata in anni n e periodicità annua k, calcola la rata periodica costante posticipata | RataMutuo[100000,4.5,10,12] |
| TassoMutuo[m,r,n,k] | dati mutuo m , rata periodica r, durata in anni n e periodicità annua k, calcola il tasso di interesse annuo effettivo | TassoMutuo[100000,1250,10,12] |
| Ammortamento[m,i,n,k] | dati mutuo m, interesse nominale percentuale annuo i, durata in anni n e periodicità annua k, calcola il piano d'ammortamento | Ammortamento[100000,4.5,10,12] |
I seguenti operatori riportano i valori immessi e prodotti.
| operatore | effetto | esempio |
|---|---|---|
| In[n] | riprende uno dei valori immessi | In[4] |
| Out[n] | riprende uno dei valori prodotti | Out[4] |
| Cancellare[nome] | annulla un'assegnazione precedente | c=1; Cancellare[c] |
I seguenti operatori producono risultati inerenti al calendario.
| operatore | effetto | esempio |
|---|---|---|
| Ora | l'orario attuale | Ora |
| Oggi | la data odierna | Oggi |
| Gs[a,m,g] | giorno della settimana corrispondente a una data espressa nella forma a,m,g | Gs[2015,3,24] |
| Jd[a,m,g] | giorno giuliano di una data espressa nella forma a,m,g | Jd[2018,3,24] |
| Giorni[{a1,m1,g1},{a2,m2,g2}] | giorni intercorrenti tra due date espresse nella forma a,m,g | Giorni[{2018,1,1},{2019,1,1}] |
| Pasqua[a] | calcola la data della Pasqua dell'anno indicato | Pasqua[2011] |
Operatori trigonometrici
| operatore | effetto | esempio |
|---|---|---|
| PoliP[r,n] | calcola il perimetro di un poligono regolare di n lati e raggio circoscritto r. | PoliP[1,7] |
| PoliA[r,n] | calcola l'area di un poligono regolare di n lati e raggio circoscritto r. | PoliA[1,7] |
| EllisseABP[a,b] | calcola il perimetro di un'ellissa dati i semiassi a e b. | EllisseABP[4,3] |
| EllisseABA[a,b] | calcola l'area di un'ellissa dati i semiassi a e b. | EllisseABA[4,3] |
| EllisseAEP[a,e] | calcola il perimetro di un'ellissa dati il semiasse maggiore a e l'eccentricità e. | EllisseAEP[4,3] |
| EllisseAEA[a,e] | calcola l'area di un'ellissa dati il semiasse maggiore a e l'eccentricitàe. | EllisseAEA[4,3] |
| Triangolo[a,b,c,α,β,γ] | risolve un triangolo dati tre elementi noti (che non siano i tre angoli): prima i tre lati, poi i tre angoli; gli elementi ignoti vanno indicati con 0) | Triangolo[10,0,0,60°,0,P/3] |
| Distanza[{la1,lo1},{la2,lo2}] | calcola la distanza in km tra due punti della superficie terrestre individuati da latitudine e longitudine o sessagesimali o decimali | Distanza[{0°,0°},{0°,1°}]; Distanza[{0,0},{0,1}] |
Espressioni matematiche
Le espressioni in input vanno scritte in linea usando la tastiera. Possono contenere numeri immediati o rappresentati da costanti, segni di operazione, funzioni predefinite o funzioni dichiarate, in entrambi i casi con argomento costante, segni di operazione e parentesi tonde eventualmente annidate e ben bilanciate.
Esempi.
P*8^2(2+3)/4(Sin[P/3])^2f1[2]+f2[Ln[2]]((10!/9!)+2)/5
Uso delle parentesi
Le parentesi si usano nel seguente modo:
tonde:
quadre:
graffe:
per contenere liste; gli elementi di una lista sono separati da virgola; sono possibili liste di liste; es. l = {{1,2},{3,4}}
Memorizzazione di costanti
Per memorizzare un valore costante se ne scrive il nome seguito da = e dal valore attribuito.
Il valore può essere un intero, un valore di verità, un razionale espresso come frazione o un decimale in virgola fissa o in virgola mobile
o una qualunque espressione contenente valori diretti, altre costanti o funzioni.
Esempi.
a = 12p = 2==3b = 1/2ln2mezzi = Ln[2]/2dati = {2,2,3,3,4,4,4,4,5,5,5,4,4,3,2,1}matrice = {{2,2,3,3},{4,4,4,4},{5,5,5,4},{4,3,2,1}}matrice = {2,2,3,3}{4,4,4,4}{5,5,5,4}{4,3,2,1})Se si definisce una nuova costante assegnandole un identificatore usato per una costante precedente, il valore precedente viene sostituito dal nuovo.
L'operatore Cancellare con argomento dato dal nome di un identificatore tra virgolette
annulla una precedente assegnazione.
Esempio.
a=1; Cancellare[a]
Dichiarazioni di funzioni reali di variabile reale e operazioni su di esse.
Per dichiarare una funzione di una o più variabili reali, se ne scrive il nome seguito
una coppia di parentesi quadre contenenti uno o più identificatori delle variabili,
da := (come in Pascal) e dall'espressione della funzione in cui eventualmente
ricompaiono gli identificatori delle variabili.
Esempi.
f[x] := x^2-1f1[x] := Sin[2x]+2Cos[x]f2[x,y] := Sqrt[x^2+y^2]Si possono inoltre definire funzioni parametriche dichiarando una funzione di una unica variabile reale come lista di funzioni di un unica variabile già definite.
Esempi.
f[x] := {Cos[x],Sin[x]}g1[x] := x^2g2[x] := x^3g[x] := {g1[x],g2[x]}Le funzioni esplicite di una variabile reale possono essere oggetto di varie procedure che richiedono almeno quattro argomenti: il nome della variabile, l'intestazione della funzione se esplicitamente dichiarata, l'inizio e la fine dell'intervallo di analisi.
Una funzione non esplicitamente dichiarata, può essere dichiarata implicitamente nell'avvio della procedura.
Di default l'intervallo viene suddiviso nel numero di punti immesso nel campo n. punti. Un quinto argomento opzionale può fissare il passo di scansione dell'intervallo.
Ricerca degli zeri. Si una l'operatore Zeri con quattro argomenti.
Esempi: f[x]:=x^2-1; Zeri[x,f[x],-2,2]Zeri[x,x^2-1,-2,2]; Zeri[x,Sin[2x],0,2P]
Ricerca dei massimi. Si usa l'operatore Massimi con quattro argomenti.
Esempi: f[x]:=x^2-1; Massimi[x,f[x],-2,2]Massimi[x,x^2-1,-2,2]; Massimi[x,Sin[2x],0,2P]
Ricerca dei minimi. Si usa l'operatore Minimi con quattro argomenti.
Esempi: f[x]:=x^2-1; Minimi[x,f[x],-2,2]Minimi[x,x^2-1,-2,2]; Minimi[x,Sin[2x],0,2P]
Produzione di un grafico. Si una l'operatore Grafico con quattro o cinque argomenti.
Esempi: f[x]:=x^2-1; Grafico[x,f[x],-2,2]Grafico[x,x^2-1,-2,2]; Grafico[x,Sin[2x],0,2P,0.1]
Esecuzione di tutte le precedenti procedure. Si usa l'operatore Studio con quattro o cinque argomenti.
Esempi: f[x]:=x^2-1; Studio[x,f[x],-2,2]Studio[x,x^2-1,-2,2]; Studio[x,Sin[2x],0,2P,0.1]
Produzione simultanea di grafici di più funzioni. Si una l'operatore Grafico con quattro o cinque argomenti.
Esempi: Grafico[x,{Sin[x],Cos[x]},0,2P]
Produzione di tabelle di una o più funzioni.
Esempio.
Tabella[x,Sin[x],0,2P]
Si possono tabulare contemporaneamente più funzioni inserendo i loro nomi in una lista delimitata da parentesi graffa.
Esempio.
Tabella[x,{Sin[x],Cos[x]},0,2P]
Grafici e tabelle sono prodotti in finestre pop-up, quindi sono visualizzabili solo se il browser in uso consente i pop-up.
Grafici di funzioni
Esempio.
Grafico[x,Sin[x],-2P,2P]
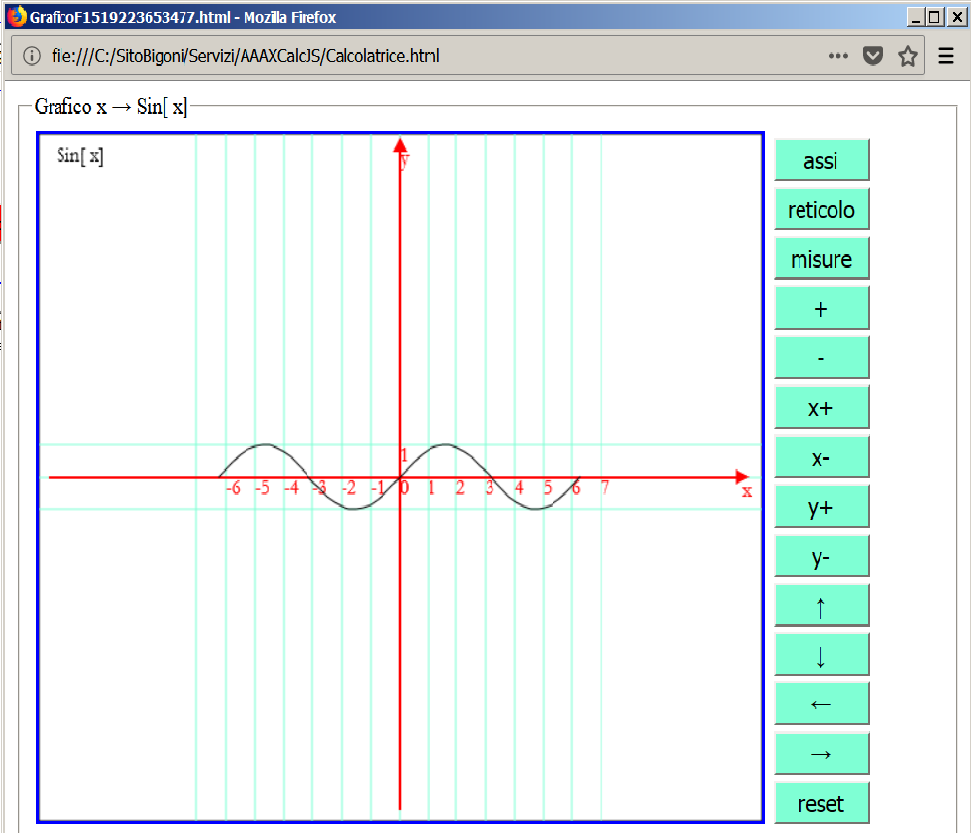
Il rettangolo contenente il grafico può può essere salvato come immagine in formato *.png in una opportuna collocazione su un supporto di memoria nel
proprio sistema (disco o memoria flash) cliccando su di esso con il pulsante destro del mouse. Negli esempi seguenti si riportano solo queste immagini.
I bottoni di fianco al rettangolo contenente grafico permettono di modificarne l'aspetto per migliorarne la resa grafica o per evidenziarne qualche caratteristica.
Ad esempio, cliccando ripetutamente il bottone ![]() , si ingrandisce il grafico.
, si ingrandisce il grafico.
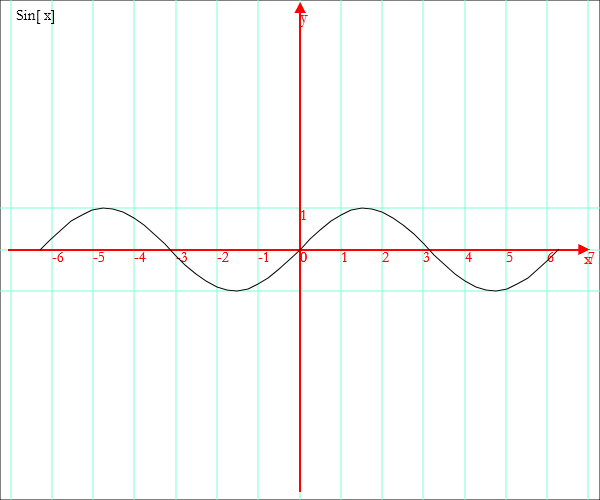
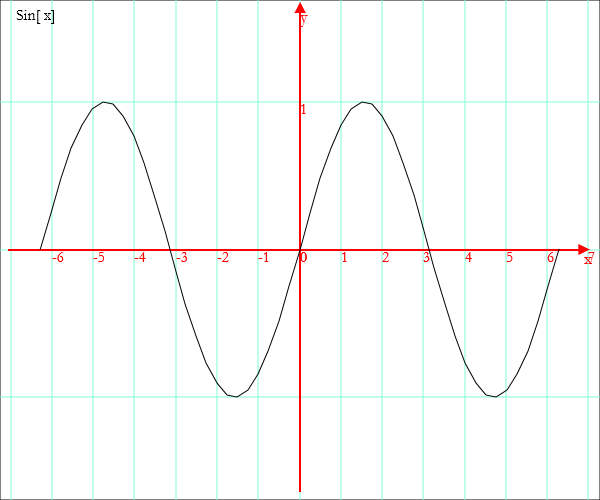
Cliccando ripetutamente il bottone ![]() , si aumenta
l'unità di misura sull'asse y.
, si aumenta
l'unità di misura sull'asse y.
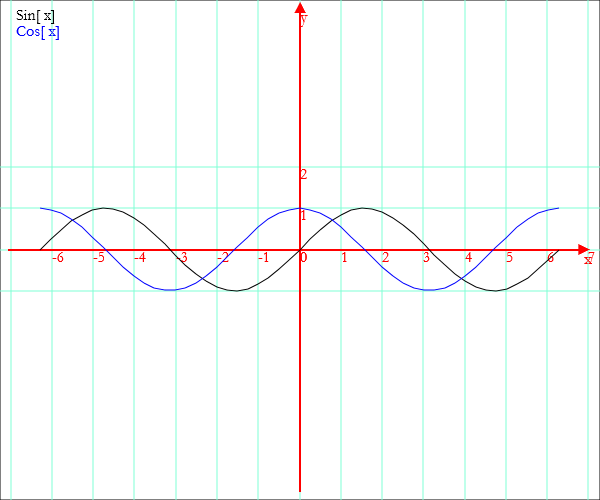
Si possono graficare contemporaneamente più funzioni inserendo i loro nomi in una lista delimitata da parentesi graffa.
Esempio.
Grafico[x,{Sin[x],Cos[x]},-2P,2P]
È possibile ottenere il grafico di una funzione precedentemente dichiarata dall'utente.
Esempio.
qsin[x]:=Sin[x]^2; Grafico[x,qsin[x],-2P,2P]
oppure, più semplicemente
Grafico[x,Sqr[Sin[x]],-2P,2P]
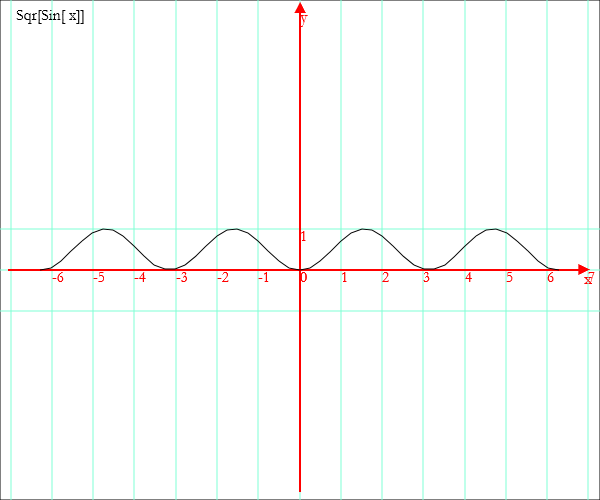
Anche in questo caso si possono graficare contemporaneamente più funzioni.
Grafico[x,{x^2-1,1-x^2},-2,2]
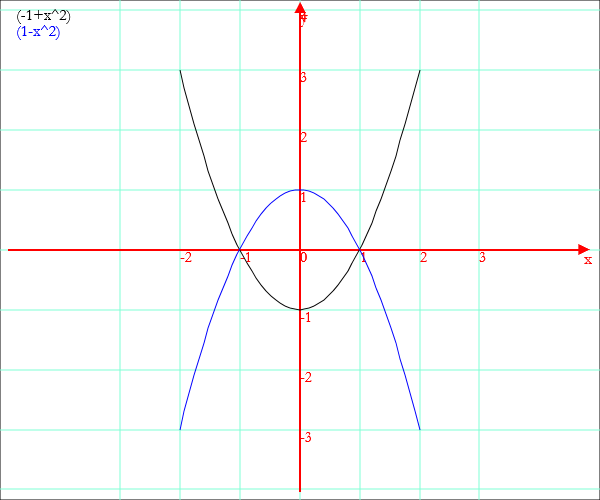
Si può definire una funzione parametrica nel seguente modo
f[x]:={x^2,x}
e graficarla
Grafico[x,f[x],-2,2]
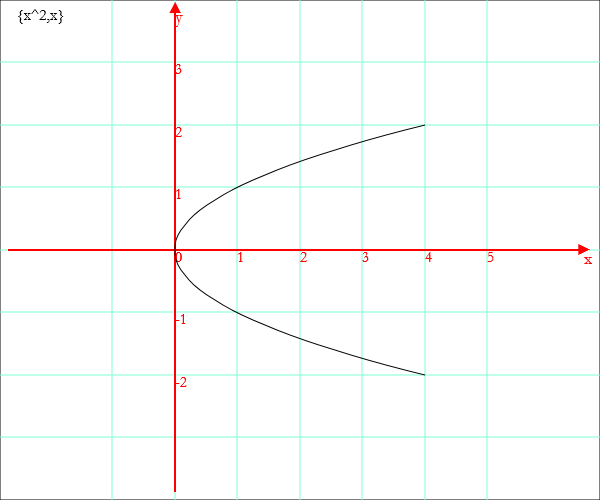
Disegni geometrici
Semplici disegni geometrici sono codificati come liste di almeno due coppie di coordinate.
Definita questa lista, il disegno viene realizzato con l'operatore Disegno.
Esempio: un segmento
Disegno[{-1,-1},{1,1}]
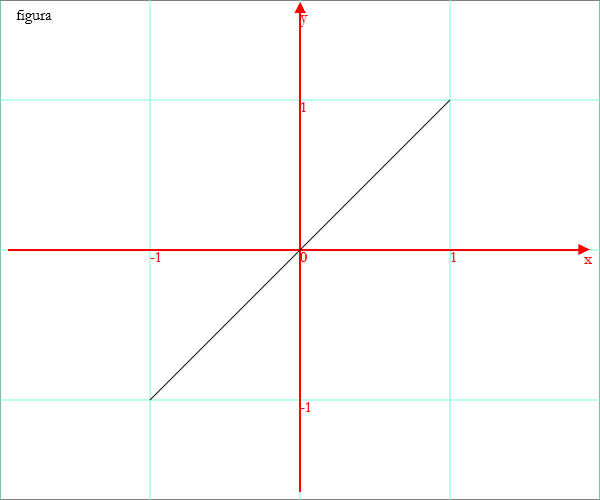
Esempio: una poligonale
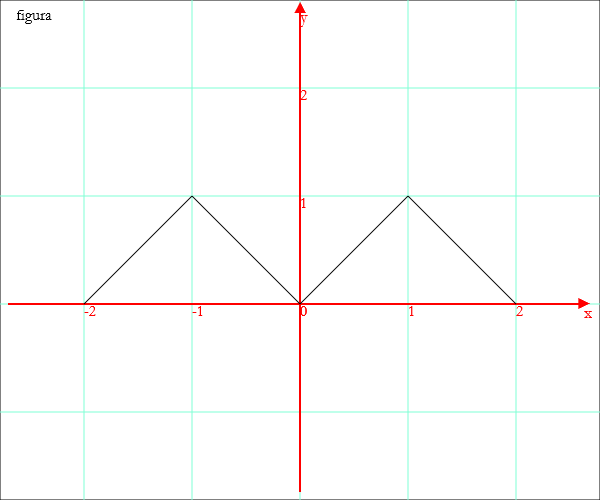
Disegno[{-2,0},{-1,1},{0,0},{1,1},{2,0}]
È possibile rappresentare poligoni regolari, circonferenze, ellissi, archi di curve definite da funzioni. Per ottenere questi risultati, bisogna operare nel seguente modo:
si genera la descrizione del disegno assegnando ad un identificatore costante il prodotto di uno dei seguenti operatori:
PoliVCircEllisseTraslazioneRotazioneDisegno con argomento uno solo o una lista di identificatori.Esempi.
penta=PoliV[{0,0},1,5]; Disegno[penta]
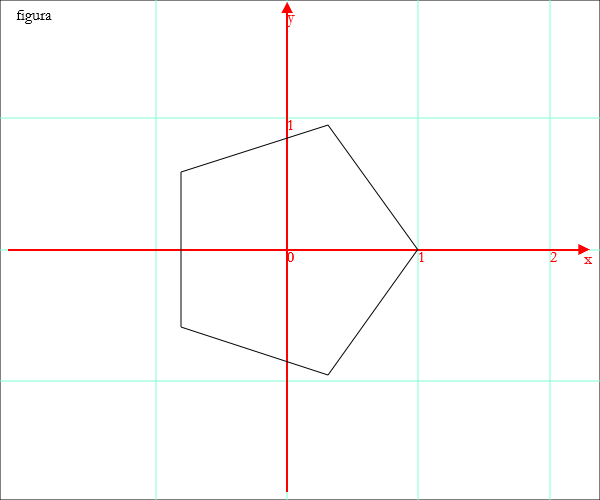
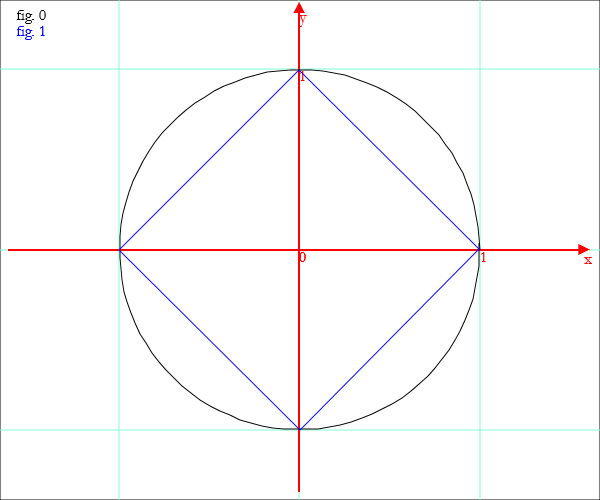
c=Circ[{0,0},1]; qu=PoliV[{0,0},1,4]; Disegno[c,qu]
Per rappresentare archi di curve descritte da funzioni reali di variabile reale si procede nel seguente modo:
si genera una lista di punti con l'operatore Coordinate applicato all'identificatore della funzione,
all'intervallo considerato ed, eventualmente, al passo di rilevazione e si assegna ad una costante il prodotto di questo operatore; es:
para=Coordinate[x,Sqr[x],-1,1,0.1]
l'identificatore dell'arco di parabola può comparire come argomento di Disegno.
Es.
para=Coordinate[x,Sqr[x],-1,1,0.1]; c=Circ[{0,0},1]; Disegno[para,c]
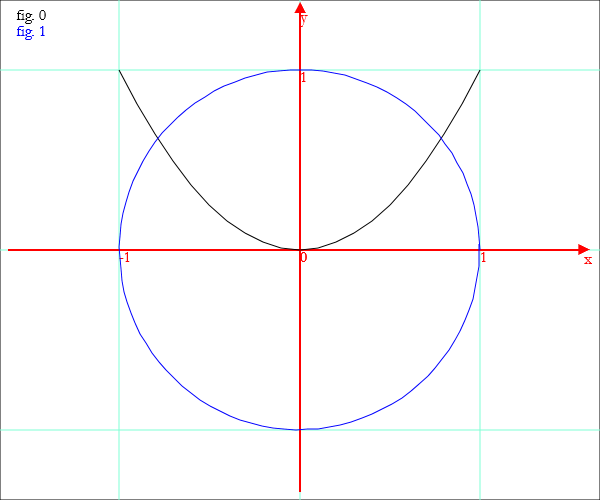
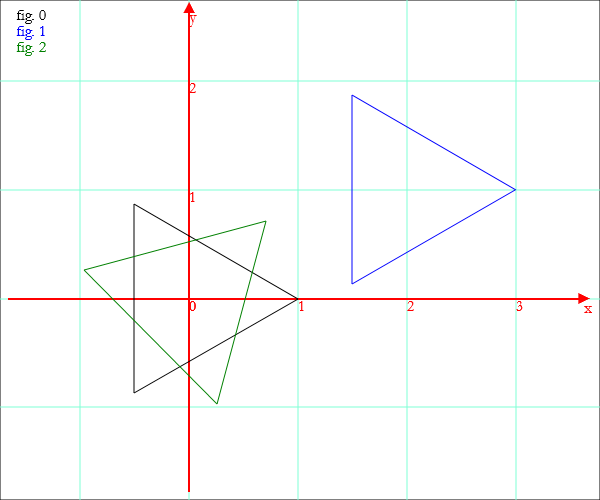
La descrizione di un disegno può essere traslata o ruotata; es:
tri=PoliV[{0,0},1,3]; trasl=Traslazione[tri,{2,1}]; rot=Rotazione[tri,45°]; Disegno[tri,trasl,rot]
Istogrammi
È possibile rappresentare istogrammi bidimensionali usando l'operatore Istogramma con argomento
costituito da una lista di coppie {numero,numero} o {stringa,numero}.
La lista deve essere preceduta da una stringa con il titolo.
Esempio.
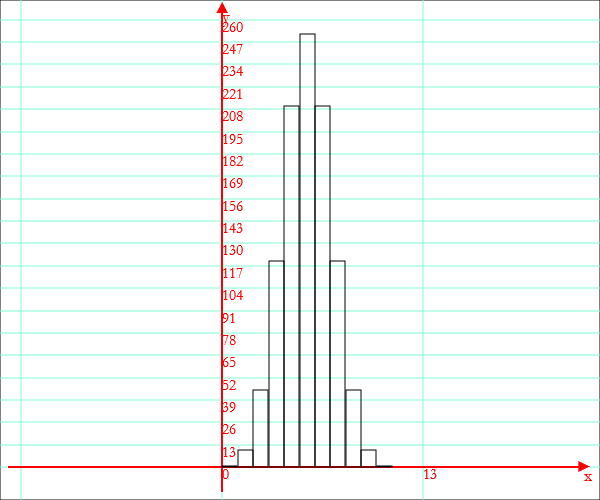
f[k] := Binomiale[10,k]; Istogramma["coefficienti binomiali",Coordinate[k,f[k],0,10,1]]
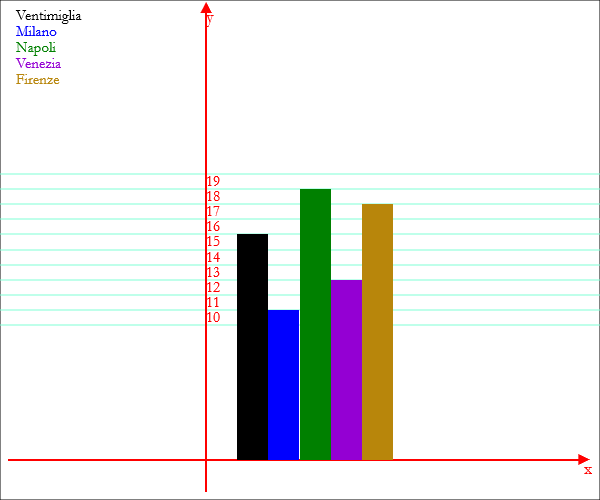
t = {"Ventimiglia",15},{"Milano",10},{"Napoli",18},{"Venezia",12},{"Firenze",17}; Istogramma["temperature",t]
ultimo aggiornamento: Maggio 2019