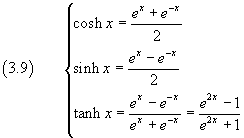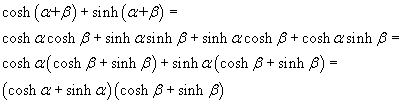
Se si sommano membro a membro le identità (2.6) si ottiene
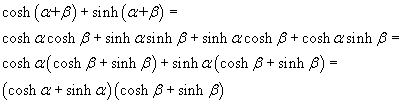
quindi
![]()
Introducendo la funzione exp(x) data dalla somma di coseno e seno iperbolici
![]()
dalla (3.1) si ottiene
![]()
Dalla (3.3) si può dedurre che la funzione exp(x) è una potenza. Essa infatti gode della proprietà tipica delle potenze: il prodotto di due potenze di ugual base è una potenza della stessa base e con esponente dato dalla somma degli esponenti.
La funzione exp(x) è detta esponenziale naturale e la sua base
![]()
è indicata con e e detta numero di Eulero (spesso nei testi italiani numero di Nepero).
Il numero e è un irrazionale trascendente il cui valore, che può essere approssimato indefinitamente con opportuni algoritmi, alcuni dei quali saranno esposti in seguito, è circa 2.71828182.
In definitiva, la funzione exp(x) può essere espressa come potenza di e
![]()
cosh x e sinh x sono definiti per ogni x ∈ R, tale e quindi anche la loro somma ex.
cosh x è sempre positivo e il suo valore assoluto è sempre maggiore di quello di sinh x, per cui ex è sempre positiva.
Se h>0, eh>1, quindi ex è sempre crescente. Infatti, per ogni h positivo,
![]()
Dato che ex è sempre crescente non ha né minimo né massimo.
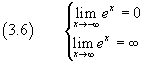
Dato che la derivata di una somma è uguale alla somma delle derivate dei suoi addendi, si ottiene che
![]()
Dalla (3.5) si ha
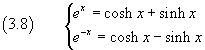
e conseguentemente