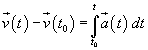
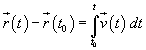
The axiomatic foundation of the Mechanics done by Newton was based not only on explicit assumptions, like the three famous principles, but also on many other implicit assumptions which can be deduced through a careful analysis of the explicit assertions.
In particular from the second principle of Dynamics we can deduce that
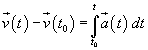
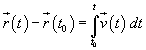
So, if we know the force that acts on a particle, the position and the velocity of the particle at a given time, we can preview with certainty the position and the velocity of the particle at whatever future time or go back to the position and the velocity of the particle at whatever moment of its past.
For instance, the knowledge of the initial position and velocity of a projectile, only under the action of its weight, is sufficient to preview with precision its trajectory.
The description of the evolution of a mechanical systems supplied by Newton implies therefore a rigid determinism: all the future is contained in the present.
But this series of deductions is based on the assumption, considered so obvious that it does not provoke any objection, that the trajectories of the bodies in motion must be geometrical curves (straight, conical, sinusoid lines, etc...). A point at a given moment occupies a very precise position, which can be described by a tern of space coordinates; all these coordinates are continuous functions, differentiable with respect to the time at least twice. It is therefore possible to define in every moment both the position and the speed of a point. This assumpion could be called, in contrast with Heisenberg's famous assumption, 'principle of determination'.
But before Heisenberg's principle, against the mechanics of Newton, based on the hypothesis of the infinite divisibility of space and time, one could have raised the ancient objections of the Eleatic philosopher Zeno. But such objections would have had very little weight in constrast to the fact that it worked. It allowed, as we all know, to deduce from the expression of the universal force of gravitation the three Kepler's laws, that constituted therefore a formidable confirmation of all the Newtonian theoretical apparatus.
The gnoseologic consequences of the work of Newton are expressed very well by the following famous excerpt of Laplace.
We ought to regard the present state of the universe as the effect of its antecedent state and as the cause of the state that is to follow. An intelligence knowing all the forces acting in nature at a given instant, as well as the momentary positions of all things in the universe, would be able to comprehend in one single formula the motions of the largest bodies as well as the lightest atoms in the world, provided that its intellect were sufficiently powerful to subject all data to analysis; to it nothing would be uncertain, the future as well as the past would be present to its eyes.
But such a rigidly determinist formulation of the interpretation of the physical phenomena cannot not interfere also with extrascientific problematics, like, for instance, the moral, legal or aesthetic ones: in a world of this kind, of which human beings are also part, can we conceive the free creativity and the free will and therefore the individual's responsibility of his own actions? Or is the human behavior fatally predetermined by multiple endogenous or exogenous factors which condition it in a necessary way so that there are no individual responsibilities?
The Newtonian foundation of the mechanics deeply influenced the European cultural movements of the 1700's and the 1800's. Such movements can be roughly grouped, with multiple intermediate degrees, around two extreme polarizations: on the one side the materialist rationalism, extrapolating methods and results of the Physics not only to the other fields of the 'Natural Philosophy', but also to all the fields of intellectual activity; on the other side the subjectivistic and spiritualistic irrationalism tending to deny cognitive value to the methods and the results of the scientific search, seen only like empirical prescriptions.