Rainbow

The rainbow is one of the more striking view offered by the nature and has been admired with astonishment by the men from the remotest antiquity. In the Bible it has been interpreted as a sign of eternal peace between God and all the creatures.

"This is the token of the covenant which I make between me and you, and every living creature that is with you, for perpetual generations: I do set my bow in the cloud, and it shall be for a token of a covenant between me and the earth. And it shall come to pass, when I bring a cloud over the earth, that the bow shall be seen in the cloud and I will remember my covenant, which is between me and you and every living creature of all flesh; and the waters shall no more become a flood to destroy all flesh. And the bow shall be in the cloud; and I will look upon it, that I may remember the everlasting covenant between God and every living creature of all flesh that is upon the earth.(Genesis 9, 12-16)."

For the ancient Greeks the rigorous and rational search into the features of the rainbow and on their causes, as a particular survey in a more general search on the nature of the light and the luminous phenomena, was undertaken by nearly all the philosophers, e.g. by Epicurus, whose doctrine was exposed in verse by Lucretius:

Hic ubi sol radiis tempestatem inter opacam
adversa fulsit nimborum aspargine contra
tum color in nigris existit nubibus arqui.
(De rerum natura: VI, 524-526)
When sun with beams amid the tempest-murk
Hath shone against the showers of black rains,
Then in the swart clouds there emerges bright
The radiance of the bow.
(translated by W. E. Leonard)

In the third book of Meteorology Aristotle gives us a description more aseptic, but much more careful and detailed of the rainbow.

The rainbow never forms a full circle, nor any segment greater than a semicircle. At sunset and sunrise the circle is smallest and the segment largest: as the sun rises higher the circle is larger and the segment smaller. After the autumn equinox in the shorter days it is seen at every hour of the day, in the summer not about midday. There are never more than two rainbows at one time. Each of them is three-coloured; the colours are the same in both and their number is the same, but in the outer rainbow they are fainter and their position is reversed. In the inner rainbow the first and largest band is red; in the outer rainbow the band that is nearest to this one and smallest is of the same colour: the other bands correspond on the same principle. These are almost the only colours which painters cannot manufacture: for there are colours which they create by mixing, but no mixing will give red, green, or purple. These are the colours of the rainbow, though between the red and the green an orange colour is often seen.
(translated by E. W. Webster)

Aristotle does not mention the fact that there is a dark band between the two bows: this band has been mentioned the first time by Alexander from Aphrodisia (approximately 200 a.D.) and today it is named 'dark band of Alexander'.

Aristotle does not notice that if the sun is high enough on the horizon, it may happen to see an inverted rainbow.

Aristotle offers, in the continuation of his book, a detailed explanation of all the things he observed, but his theory turns out to be inadequate for two reasons:

It can be interesting to observe that the aristotelian opinion on the number of the colours of rainbow (three or four) was accepted passively until Newton (1643-1727), studying the decomposition of the solar light by a prism, counted seven colours.

The topic, in the classical antiquity, was resumed by other authors: we remember the works on the optics of Euclid and Tolomaeus.

While in the Middle Ages in Europe the greater part of the scholars continued to passively accept the opinions of the ancient philosophers, disputing whether the number of the colours were three (like the persons of the Holy Trinity) or four (like the four elements of Empedocles) a great Arab scientist, Ibn Al Haytham (965-1038), known in Europe as Alhazen, improved a lot the understanding of the topic discovering the phenomenon of the refraction, even if he did not succeed in discovering its law.

Meanwhile (maybe some link existed between East and West), the work of Alhazen, translated in Latin (De aspectibus or Perspectiva), was resumed by Roger Bacon (Opus maius) who in 1266 found that the measure of the angle of the rainbow is 42° (the secondary one is 8° degrees higher in the sky). In 1304 the german monk Dietrich von Freiberg (Theodoricus Teutonicus de Vriberg: De iride) proposed the hypothesis that every water drop in the clouds makes its own rainbow and verified his hypothesis by the observation of the diffraction of the solar light in a spherical bottle of water. The discoveries of Dietrich remained unknown during three centuries. His results were rediscovered at the beginning of the seventeenth century by Marco Antonio de Dominis in 1611, by Descartes in 1637 and, independently, by Giovan Battista Hodierna (1647).

Descartes simplified the study of the rainbow reducing it to the study of a water drop and of the way with which it interacts with the light that hits it and could apply the mathematical formulation of the law of the diffraction exposed by W. Snell in 1621.

A bit of mathematics.

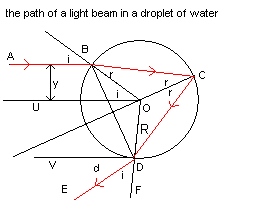
Following the theory proposed by Descartes, we consider a single beam of solar light AB, by hypothesis monochromatic and horizontal: as reported by Aristotle, we see the rainbow when the sun is not too much high in the sky: when there is the rainbow, in first approximation, the solar beams can be considered to be parallel to the horizon.
The beam has distance y from the horizontal line UO passing for the center or of the sphere. y is the impact parameter. If we call R the radius of the sphere, we have

The beam penetrates in the sphere in the point B and forms an angle of incidence of measurei with the straight line perpendicular to the surface, the the radial line OB, and is refracted following the line BC which forms an angle of refraction of measure r with the line OB.

where n is the index of refraction of the water for the considered colour.
We get therefore

The beam hits the surface of the sphere in C. Some energy of the beam goes out from the sphere, some other energy is reflected following the line CD which, for the law of the reflection, forms an angle of measure r with the radius OC.

The beam CD hits the surface of the sphere in D and again some energy is reflected and some goes out following the line DE which forms an angle of measure i with the radius OD. The part which goes out, hitting the eye of the observer, originates the primary rainbow. The reflected part will hit again the internal surface of the sphere and will be again partially reflected end partially refracted. The refracted part goes out from the sphere. This second emission originates the secondary rainbow. In order not to complicate too much figures and calculations, we analyze here only the formation of the primary rainbow.

The beam DE and the horizontal line DV form the angle VDE, the measure of which is d; this measure can be obtained for difference between those of the angles FDV and FDE, which is i.

In its turn the measure of FDV, for parallelism, is equal with that of FOU.
The measure of FOU can be obtained for difference between the measures of BOD and BOU.
But BOD is the double of BCD, so it has measure 4r and BOU measures i.
We get therefore

The deflection does not depend on the radius R of the sphere, but only on the index of refraction n and, since this index varies with respect to the wavelength λ, each colour has its angle of greatest deflection. Therefore a water drop, like a prism, produces the dispersion of the colours.

The parameter y varies from 0 to R; if we graph d with respect to y in this interval, for n=1.33 which is the index of refraction of the red colour in the water, we get:

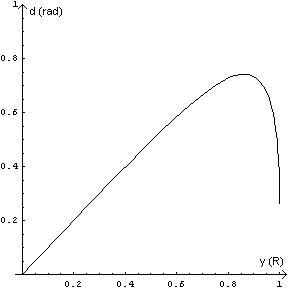
The deflection angle d grows to growing of y and catches up a maximum around 9/10 of the radius; this maximum is approximately 0,75 radians, i.e. about 42°. None of the solar beams has greater deflection: physically this means that when we watch the sky over the rainbow, we cannot receive any light. There is the dark band of Alexander.

By equating to zero the first derivative of d with respect to y we can obtain more exactly the value of the parameter y with greatest deflection and therefore the value of such deflection.

If we calculate the greatest angle of dispersion for some colours, we get the following values:

λ (nm)	colour	n	d_max (rad)	d_max (deg)
706,5	red	1,3300	0,742051	42°30'59"
589,3	yellow	1,3330	0,734402	42°04'41"
501,6	green	1,3364	0,725817	41°35'10"
404,7	violet	1,3427	0,710143	40°41'18"

To learn more...

If you extend the method we have exposed, you can explain also the secondary rainbow and its features as described by Aristotle and R. Bacon.

But the results obtained with the method of Descartes, based on the simple laws of geometric optics, cannot explain other important phenomena like e.g. the supernumerary bows, the intensity of the colours, the polarization of the light.

Many physicists in 18th century (Young) and in 19th century (Airy) devoted themselves to the study of these features. The research continues today developing sophisticated mathematical models based on the ondulatory theory of the light and on the quantum mechanics.

You can find interesting reports on these researches and experiments you can do yourselves in:

Some bits of history.

A bit of mathematics.

To learn more...