(notes by R. Bigoni - home italian)
In 1610, Galileo discovered the four largest Jupiter satellites: Io, Europa, Ganymede and Callisto.
The orbits of these satellites have a vary small eccentricity (for example, the eccentricity of Io is 0.00041); so their motion can be considered with good approximation circular and uniform. Furthermore the orbits are very close to the equatorial plane of Jupiter. The equator of Jupiter and its own orbit have a very small inclination with respect to the eclyptic plane so, when seen from the Earth, the four satellites, at every revolution,
Eclipses and occultations are different phenomena: an eclipse can begin before a successive occultation and finish during the occultation, so its end cannot be seen from the Earth; in an analogous way an eclipse can begin during an occultation and finish after the end of the occultation.
You may see a nice Java applet that shows the motion of Jupiter's satellites at The Castle Point Astronomy Club.
The motions of these satellites are so regular that Galileo thought that the accurate registration of them could have not only scientific but also practical interest with respect to a most important problem not still resolved around the beginning of the 17th century, that is the measure of the longitude. But Galileo could not carry out his idea for the lack of reliable clocks.
The aim of Galileo was successfully realized in 1668 by Cassini who could make use of better astronomical instruments and of the clock invented by Huygens(1657).
In the winter of 1671-1672, Picard and Roemer (at Uraniborg, the observatory of Tycho Brahe on the island of Hven, (then in Denmark, now in Sweden) and Cassini (at the observatory of Paris), simultaneously measured the beginning of an eclipse of Io. From this measurement they could calculate the difference of the longitude between Uraniborg and Paris.
From 1672 Roemer was at the observatory of Paris and, continuing the observation of the eclipses of Io, found that the intervals of time between two successive beginnings (or endings) of the eclipses resulted different around the year: when the Earth was moving away from Jupiter they were greater than when the Earth was moving nearer to Jupiter.
Thanks to this discovery Roemer could demonstrate that the speed of light is finite and put an end to a controversy that divided the european scientists in the 17th century: on one side there were those, like Kepler, Descartes, Cassini, who, following the opinion of Aristotle, believed that the speed of light is infinite; on the other side there were those, like Galileo, who believed the contrary but couldn't experimentally validate their persuasion.
Roemer published his results in 1676.
Here we apply the method of Roemer to a set of data collected in 1995.
For simplicity's sake, we assume that the Earth's orbit around the Sun is circular.
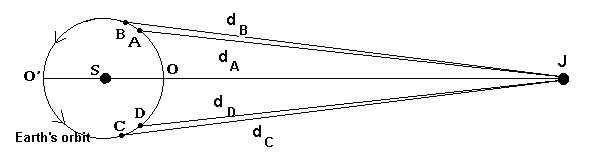
When the Earth is in O, Jupiter (J) is in opposition to the Sun.
When the Earth is in O', Jupiter is in conjunction to the Sun.

Furthermore we assume that if the displacements of the Earth are small, Jupiter can be considered as immobile.
Time intervals between the beginnings (or the endings) of two consecutive eclipses of Io in the shadow of Jupiter result constant if the measurements are made when the Earth is near O or O': in these cases one obtains
![]()
But when the Earth is in an intermediate place between O and O', for example in the point A (between an opposition and a conjunction) or in the point C (between a conjunction and an opposition) time intervals measures are greater (in A) or lesser (in C) than those ones made near O or O'.
It must be noted that when the Earth is between an opposition and a conjunction (A) we can see only the endings of the eclipses; vice versa, when the Earth is between a conjunction and an opposition, we can see only the beginnings.
Roemer understood that the different results were ascribable to the relative motion of the Earth with respect to Jupiter and to the finiteness of the speed of light.
The Earth's radial motion relative to Jupiter is unimportant when the Earth is near O or O', but it is noteworthy in the intermediate positions. When the Earth is in A, it is going away from Jupiter; when it is in C it is approaching the big planet.
If t is the instant of the end of an eclipse of Io and in this moment the Earth is in A, at the end of the following eclipse the Earth, rotating counterclockwise, reaches the point B.
Since the speed of light c is finite, from the Earth the end of the eclipse in A isn't seen at the time t but at the time
![]()
where
![]() is the time needed by light to cover the distance dA.
is the time needed by light to cover the distance dA.
The end of the following eclipse isn't detected at the time t+T but at the time
![]()
therefore the time interval TAB between two successive eclipses, measured by a terrestrial observator, results
![]()
If t is the instant of the beginning of an eclipse of Io and at this time the Earth is in C, the following eclipse will begin when the Earth will reach the point D.
In this case the beginning of the eclipse is seen from the Earth at the time
![]()
and the beginning of the following eclipse is detected at the time
![]()
therefore the time interval TCD between the two eclipses results
![]()
We have seen at the point a) of the previous section that, when the Earth is between an opposition and a conjunction, the time interval between two successive eclipses in A and B, as measured by a terrestrial observator, is
![]()
Let C, D, E,... be other successive points of the Earth's orbit between the same opposition and the same conjunction. In an analogous way we shall have
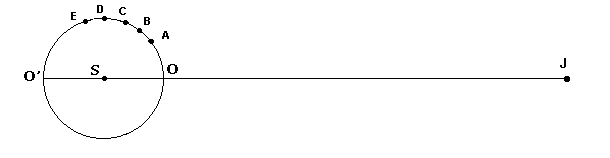
![]()
![]()
![]()
The sum of the left sides of the equalities gives
![]()
therefore
![]()
If we apply this procedure to the data of the following table, reporting the times of the ends of 99 eclipses registered between an opposition of Jupiter to the Sun and the following conjunction, we obtain with good approximation,
![]()
where the expression between parentheses represents the time Δ elapsed between the first and the last observation (times are in the form dd/mm/yy,hh.mm), T is the orbital period of Io and au is the astronomical unit, that is the semi-major axis of Earth's orbit.
Δ amounts to 14986680 seconds, 98 T amounts to 14985670 seconds. The difference Δ-98 T amounts to 1010 seconds. The astronomical unit is about 1.5·1011m.
Therefore we obtain
![]()
| ord. | date | time | ord. | date | time | ord. | date | time |
|---|---|---|---|---|---|---|---|---|
| 00 | 02/06/95 | 08h06 | 34 | 01/08/95 | 12h20 | 68 | 30/09/95 | 16h40 |
| 01 | 04/06/95 | 02h34 | 35 | 03/08/95 | 06h48 | 69 | 02/10/95 | 11h09 |
| 02 | 05/06/95 | 21h03 | 36 | 05/08/95 | 01h17 | 70 | 04/10/95 | 05h37 |
| 03 | 07/06/95 | 15h31 | 37 | 06/08/95 | 09h56 | 71 | 06/10/95 | 00h06 |
| 04 | 09/06/95 | 10h00 | 38 | 08/08/95 | 14h15 | 72 | 07/10/95 | 18h35 |
| 05 | 11/06/95 | 04h28 | 39 | 10/08/95 | 08h44 | 73 | 09/10/95 | 13h04 |
| 06 | 12/06/95 | 22h57 | 40 | 12/08/95 | 03h12 | 74 | 11/10/95 | 07h33 |
| 07 | 14/06/95 | 17h25 | 41 | 13/08/95 | 21h41 | 75 | 13/10/95 | 02h01 |
| 08 | 16/06/95 | 11h54 | 42 | 15/08/95 | 16h10 | 76 | 14/10/95 | 20h30 |
| 09 | 18/06/95 | 06h22 | 43 | 17/08/95 | 10h39 | 77 | 16/10/95 | 14h59 |
| 10 | 20/06/95 | 00h51 | 44 | 19/08/95 | 05h08 | 78 | 18/10/95 | 09h28 |
| 11 | 21/06/95 | 19h20 | 45 | 20/08/95 | 23h26 | 79 | 20/10/95 | 03h57 |
| 12 | 23/06/95 | 13h48 | 46 | 22/08/95 | 18h05 | 80 | 21/10/95 | 22h26 |
| 13 | 25/06/95 | 08h17 | 47 | 24/08/95 | 12h34 | 81 | 23/10/95 | 16h54 |
| 14 | 27/06/95 | 02h45 | 48 | 26/08/95 | 07h03 | 82 | 25/10/95 | 11h23 |
| 15 | 28/06/95 | 21h14 | 49 | 28/08/95 | 01h32 | 83 | 27/10/95 | 05h52 |
| 16 | 30/06/95 | 15h43 | 50 | 29/08/95 | 20h00 | 84 | 29/10/95 | 00h21 |
| 17 | 02/07/95 | 10h11 | 51 | 31/08/95 | 14h29 | 85 | 30/10/95 | 18h50 |
| 18 | 04/07/95 | 04h40 | 52 | 02/09/95 | 08h58 | 86 | 01/11/95 | 13h18 |
| 19 | 05/07/95 | 23h09 | 53 | 04/09/95 | 03h27 | 87 | 03/11/95 | 07h47 |
| 20 | 07/07/95 | 17h37 | 54 | 05/09/95 | 21h56 | 88 | 05/11/95 | 02h16 |
| 21 | 09/07/95 | 12h06 | 55 | 07/09/95 | 16h25 | 89 | 06/11/95 | 20h45 |
| 22 | 11/07/95 | 06h35 | 56 | 09/09/95 | 10h54 | 90 | 08/11/95 | 15h13 |
| 23 | 13/07/95 | 01h03 | 57 | 11/09/95 | 05h22 | 91 | 10/11/95 | 09h42 |
| 24 | 14/07/95 | 19h32 | 58 | 12/09/95 | 23h51 | 92 | 12/11/95 | 04h11 |
| 25 | 16/07/95 | 14h01 | 59 | 14/09/95 | 18h20 | 93 | 13/11/95 | 22h40 |
| 26 | 18/07/95 | 08h30 | 60 | 16/09/95 | 12h49 | 94 | 15/11/95 | 17h09 |
| 27 | 20/07/95 | 02h58 | 61 | 18/09/95 | 07h18 | 95 | 17/11/95 | 11h37 |
| 28 | 21/07/95 | 21h27 | 62 | 20/09/95 | 01h47 | 96 | 19/11/95 | 06h06 |
| 29 | 23/07/95 | 15h56 | 63 | 21/09/95 | 20h15 | 97 | 21/11/95 | 00h35 |
| 30 | 25/07/95 | 10h24 | 64 | 23/09/95 | 14h44 | 98 | 22/11/95 | 19h04 |
| 31 | 27/07/95 | 04h53 | 65 | 25/09/95 | 09h13 | |||
| 32 | 28/07/95 | 23h22 | 66 | 27/09/95 | 03h42 | |||
| 33 | 30/07/95 | 17h51 | 67 | 28/09/95 | 22h11 |
last revision: 23/10/2015