If we consider the equation (6.5)
which represents a state of a particle bouncing between two walls and differentiate twice Ψn with respect to x, we obtain
From (6.7) we have
so (7.1) becomes
Introducing the symbol
(said Dirac constant or reduced Planck constant) in (7.3), we get
Since the equality (7.5) holds for every n, we can write
The partial differential equation (7.6) is said Schrödinger equation of the analyzed physical system.
The Schrödinger equation plays a fundamental role in the study of the behavior of atomic and subatomic particles called Quantum Mechanics. It is as important as the Newton laws in Classical Mechanics.
The (7.6) is a very simple expression of the Schrödinger equation, because it applies only a static, one-dimensional system without potential energy. More generally, if a static system is three-dimensional and has potential energy, the Schrödinger equation must be written as
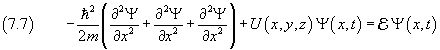
Finally, to simplify the notation, we can introduce the symbol H, said Hamiltonian operator,
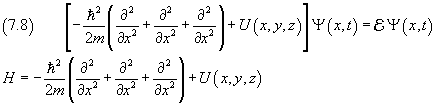
In conclusion, to understand the behavior of a physical system, one writes and tries to resolve the equation
(7.9). The solution of this equation allows to obtain the values
,
called eigenvalues of the operator H, and the functions Ψn, called eigenfunctions
or eigenstates of H.