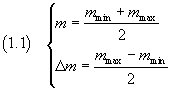
Note by Roberto Bigoni
The exact measure of a physical quantity is a theoretical concept experimentally inaccessible and therefore devoid of experimental meaning.
In the experimental practice we can directly estimate only the smallest and the largest values mmin and mmax of the measure M, so we can only say that M is in the range [mmin,mmax].
If we denote by
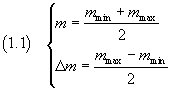
we can express the informations on the measure M in the following way
![]()
where u represents the unit of measure and depends on the system of units
we have adopted.
The parameter Δm is commonly called absolute uncertainty.
The value of Δm defines the number of significant digits with which it makes sense to express M, that is the last significant digit of M must have the same order of magnitude as Δm.
For example, does not make sense (and therefore should be avoided) say that a measure of length is
![]()
because the absolute uncertainty blurs the evaluation of the millimeters so the digits relating to tenths and hundredths of a millimeter are meaningless.
For this reason it is good practice to round the absolute uncertainty to one significant digit and to express as the last significant digit of the mean value the digit affected by the absolute uncertainty.
The measure of the example must be properly written
![]()
To measure directly the values of m and Δm we usually compare M with predetermined values provided by a tool consisting essentially of a graduated rule. For example, to measure a length we use a ruler or a vernier caliper; to measure a duration of time we use a stopwatch; to measure a current we use an ammeter.
In this comparison we may be faced with two different occurrences:
When repeating the measurement, we always get the same result (this happens if we use instruments with low precision), we assign to m the reading on the instrument and to Δm the value of the smallest division readable on the instrument.
When, repeating the measurement we get many values randomly different (this happens if we use instruments with
high precision) we assign to m the mean value and to Δm three times the
sample standard deviation (σ).
The analysis of random distributions due to Gauss shows that the probability that a measure is between
m-3σ and m+3σ is very close to 1.
The ratio ![]() is said
relative uncertainty.
is said
relative uncertainty.
The relative uncertainty expresses the goodness of the measure.
A small relative uncertainty means that the measure is very accurate; a large relative uncertainty implies that the measure is unreliable or even unusable.
From the knowledge of the mean value and its uncertainty, we can derive the absolute uncertainty:
![]()
For example, if calculating the extent of an area we have obtained
![]()
and the relative uncertainty is 0.0123, we get
![]()
then the measure must be written
![]()
Given the mean values and the absolute uncertainties of two homogeneous quantities A and B
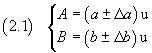
(u represents the the common unit of measure of the two quantities
that later will be understood for the sake of clarity of the text)
the smallest and the largest value of their sum S are
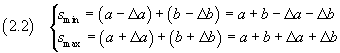
therefore, from the equations (1.1), the mean value and the absolute uncertainty of S are
![]()
that is
the absolute uncertainty of a sum is the sum of the absolute uncertainties of the addends.
The smallest and the largest value of their difference D are
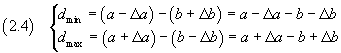
The smallest value of D is obtained from the smallest value of A minus the greatest value of B; the greatest value of D is obtained from the greatest value of A minus the smallest value of B.
Therefore, from the equations (1.1), the mean value and the absolute uncertainty of D are
![]()
that is
the absolute uncertainty of a difference is the sum of the absolute uncertainties of their terms.
Given the mean values and the absolute uncertainties of two quantities A and B
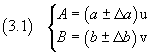
(u and v represent the units of measure, possibly coinciding, of the two
quantities that later will be understood for the sake of clarity of the text)
the smallest and the largest value of their product P are
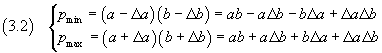
Since the products ΔaΔb, for significant measures, are of order of magnitude much smaller than those of the other addends, these products can be neglected; we can consequently write
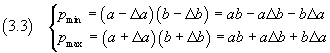
therefore, from the equations (1.1), the mean value and the absolute uncertainty of P are
![]()
From (3.4) we obtain
![]()
that is
the relative uncertainty of a product is the sum of the relative uncertainties of its factors.
As an immediate corollary we have that
the relative uncertainty of a power is the product of the exponent for the relative uncertainty of the basis.
The smallest and the largest value of their ratio Q are
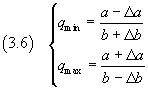
The minimum value is obtained from a minimum of A divided by the maximum value of B, the maximum value is obtained from the maximum value of A divided by the minimum value of B.
From the equations (1.1), the mean value and the absolute uncertainty of Q are
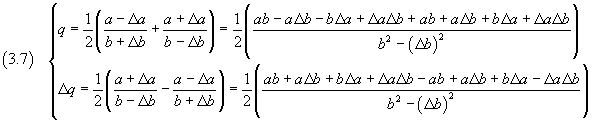
If we simplify and neglect the products and the powers of the absolute uncertainties, we obtain
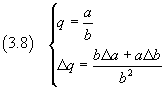
From (3.8) we have
![]()
that is
the relative uncertainty of a ratio is the sum of the relative uncertainties of its terms.
last revision: June 2018