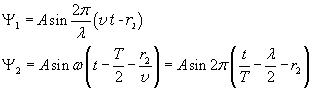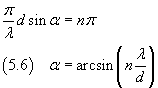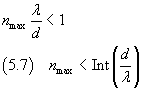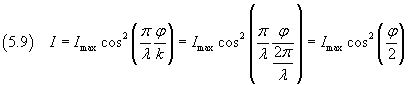Interference.

If a point P of a continuous and elastic medium is hit by two waves Ψ₁ and Ψ₂, emitted by two different sources O₁ and O₂, from which it has distances, respectively, r₁ and r₂, it oscillates as if it were hit by a single wave Ψ resulting from the sum of Ψ₁ and Ψ₂.

• If O₁ and O₂ oscillate in phase with equal amplitudes and equal angular frequencies, using the prosthaphaeresis formulas, we obtain

  

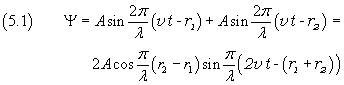
  The amplitude of Ψ is

  

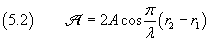
  This amplitude takes its maximum value 2A, when the absolute value of the cosine of in the equation (5.2) is 1, ie when

  

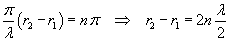
  The points P of the medium, for which the absolute value of the difference between the distances from O₁ and O₂ is equal to an even number of half wavelengths, oscillate with the greatest amplitude.

  Instead, the resulting amplitude vanishes, ie the point P does not oscillate, when the cosine is zero, ie when

  

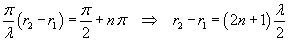
  The points P of the medium, for which the absolute value of the difference between the distances from O₁ and O₂ is equal to an odd number of half wavelengths, does not oscillate.

  In general, when there are two sources with these characteristics, the points of the medium oscillate with different amplitudes, ranging from a maximum 2A to a minimum 0.

  All the adjacent points which do not fluctuate form hyperboloidal surfaces called nodal surfaces. The points that oscillate with greatest amplitude form hyperboloidal surfaces said antinodal surfaces.

  If the two waves are one-dimensional, that is, if they propagate in a straight line medium, nodal and antinodal surfaces become points called nodes and antinodes.

  In this case, the midpoint between two sources is an antinode.

• If instead the sources O₁ and O₂ are half cycle out of phase, that is, to give the idea, they oscillate as the opposite dishes of a balance, the wave functions, with a suitable choice of the start time, are

  

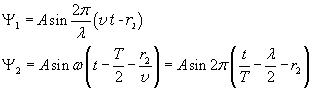
  Everything works as if the sources oscillate in phase but with the source O₂ at a distance increased by half a wavelength.

  Therefore, the situation is reversed with respect to the previous case: now the points P are nodes when the absolute value of the difference between their distances from O₁ and O₂ is equal to an even number of half wavelengths. Instead we find antinodes in points P such that the difference between their distances from O₁ and O₂ is equal to an odd number of half wavelengths.

  In this case, the midpoint between two sources is a node.

• If the two sources oscillate with slightly different frequency, the phenomenon of beats occurs, that is a periodic variation of the amplitude of the resultant wave.

  animation

   

Interference of light

If we project a beam of polarized monochromatic light on an opaque diaphragm, in which were made two thin straight slits, parallel to each other and perpendicular to the plane of polarization of the light and behind the diaphragm we put a white screen, at a distance large enough so we can consider this distance infinite with respect to the distance d between the slits, we observe on the screen not just two bright stripes corresponding to the slots, as one would expect based on the principles of geometrical optics, but a series, which could be very large, of bright stripes separated by dark stripes.

These strips are called interference fringes and they can be explained, only admitting that the light is a wave. In fact, on the basis of experiences of this kind, made by T. Young, the physicists of the nineteenth century, rejected the hypothesis, supported by Newton, that light is made up of small discrete particles.

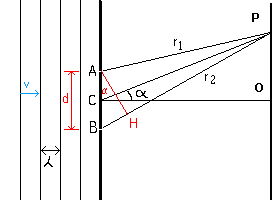
By accepting the Huygens' principle, we interpret the slits A and B of the figure, reached at the same time by the same wavefront, as sources of elementary cylindrical waves, which interfere in the point P of the screen OP, having distances r₁ from A and r₂ from B.

If O is the point of the screen on the geometrical axis CO of the segment AB, and we denote by d the length of the segment AB and by α the angle OCP and assume that the distance CO is infinite with respect to d, we have

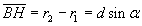
From the equation (5.2) we have

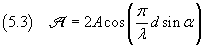
The maximum of the amplitude A_max is reached when α=0 and is 2A, so

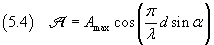
The intensity, which is visually perceived as light intensity, from the equation (3.26), is proportional to the square of the amplitude, thus

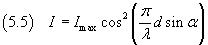
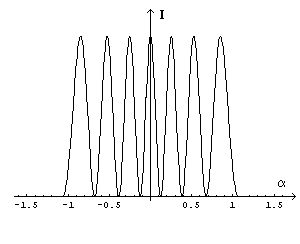
The intensity of the strip has its maximum when the absolute value of the cosine is 1, ie if

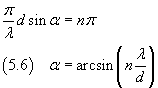
From the equation (5.6) we can see that our calculations make sense only if λ<d. Moreover, if n_max is the maximum value of n,

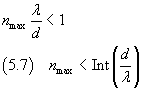
then in the equation (5.6) n takes integer values from -n_max to n_max so will see 2n-1 bright fringes separated by dark fringes. In the example shown in the graph below we assume λ = 1/4 d.

If we represent by φ the phase shift between the two waves emitted by A and B in a point on the screen

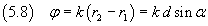
the equation (5.5) can be rewritten as

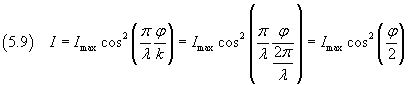
The equation (5.9) expresses in general the intensity due to interference of waves of equal amplitude and angular frequency and with a mutual phase shift φ.
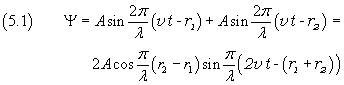