Spherical zones and caps

Notes by R. Bigoni
(from Note Didattiche)

1. Spherical zone

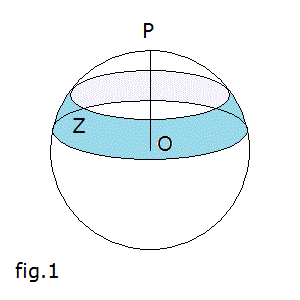
Given a spherical surface Σ with center O and radius OP with measure R, two parallel planes φ and ψ such that their distance from the center O is smaller than R, intersect Σ in two circumferences.
The region of Σ bounded by these circumferences is called spherical zone Ζ. The circles enclosed by these circumferences are its bases.

To calculate the surface of a spherical zone we can proceed in the following way:

• let's draw from O a straight line OQ perpendicular to OP;

  

• we consider the intersections between Σ, φ and ψ with the plane Π of these two perpendicular lines;

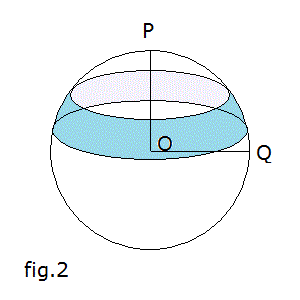
• we assume the straight line OQ as the axis of the abscissas and the line OP as the axis of the ordinates;

  

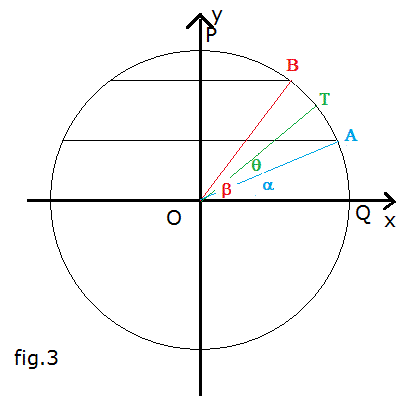
• the points A and B are respectively the intersections in the first quadrant between γ and the planes φ and ψ; T is any point of γ;

  the radiuses OA, OB and OT form, respectively, the angles α, β and θ with the positive direction of the x axis;

  the coordinates of A, B and T are respectively

  

• an infinitesimal segment dγ of γ has length

  

• the area S of the zone Z can be conceived as the sum of the lateral surfaces of cylinders of infinitesimal height dγ and base radius with θ from α to β;

  

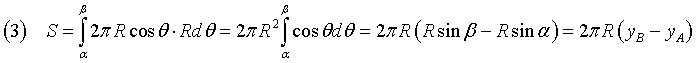
• if we represent by δ the distance between the planes φ e ψ

  

  we get

  

2. Spherical segment

With reference to fig. 1, the solid Ω bounded by the spherical zone Z and its bases is called spherical segment.

With reference to fig. 3 and with a method similar to that used for the calculation of S, the volume V of Ω can be calculated as the sum of the volumes of the cylinders with infinitesimal height dy and base radius with y from y_A to y_B;

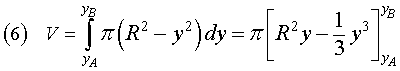
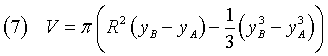
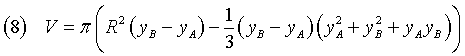
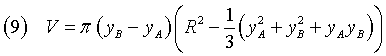
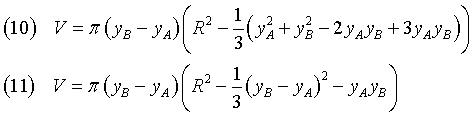
From the equation (4) we get

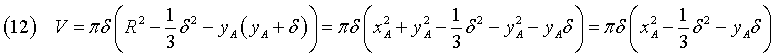
Moreover, if we apply the Pythagorean theorem

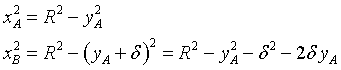
and subtract side by side

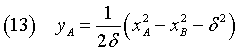
If we plug this expression for y_A into the equation (12)

3. Spherical cap

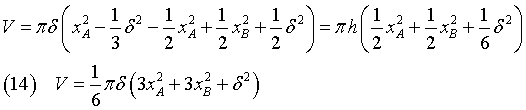
If in fig. 1 the plane most distant from the center is tangent to Σ in P, the resulting figure is said spherical cap.

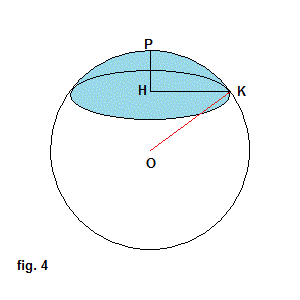
In fig. 4, H is the center of the base of the cap, P is its vertex, the segment HK is the radius of the base with measure r, the segment HP is the height of the cap with measure δ and OK is the radius of Σ with measure R.

The equation (5) allows the calculation of the outer surface of the cap

Th equation (14) with x_A=r and x_B=0 gives the volume of the cap

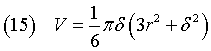
If we apply the Pythagorean theorem, we get

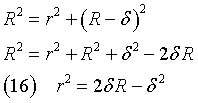
and, plugging this expression for r² into the equation (15), we obtain

3. Visible cap of a spherical surface.

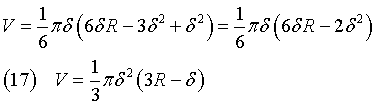
Given a spherical surface Σ with center O and radius R and the point E outside Σ at distance h from it, the portion of Σ observable from E is a cap whose area can be calculated as follows:

• we consider the cone Γ with vertex in E, with lateral surface tangent to Σ and base formed by the set of tangency points;

• we represent the intersections of Σ and Γ with a plane passing through the line OE;

  

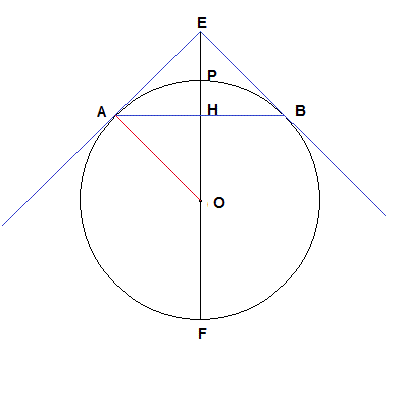
  the section of Σ is a circumference; the section of Γ is an isosceles triangle with vertices E, A and B;
  the height of the triangle lies on the line of the diameter EF, intersects the circumference in P and intersects the base in H;

• the triangle EAO is right-angled in A;

• the triangle EAO is similar to the triangle AHO

  

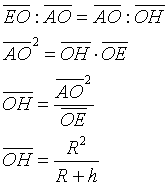
• in the cap we have

  

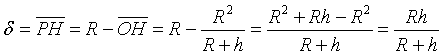
• and finally, from the equation (5),

  

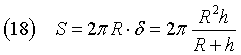
The surface of Σ is S=4πR², hence the fraction of Σ visible from E is

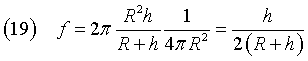
last updated: March 16, 2018