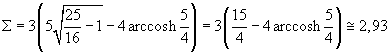
(notes by R. Bigoni)
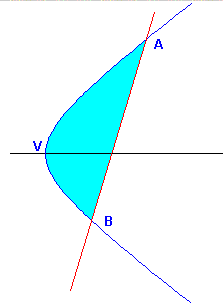
Given in a plane Π the hyperbola γ and the straight line r which intersects a branch of γ in two points A and B, the figure S delimited by the arc AB and by the chord with the same endpoints is called hyperbolic segment.

In particular, if r is perpendicular to the axis of γ, S is said to be right.
In order to calculate the area Σ of the right hyperbolic segment formed in the cartesian reference frame Oxy by the hyperbola γ with canonical equation
![]()
and by the straight line r with equation
![]()
we can act in the following way.
We apply to the curves the linear transformation which transforms γ into the equilateral hyperbola with unitary real semiaxis
![]()
This transformation has matrix
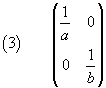
Therefore the transformed straight line has equation
![]()
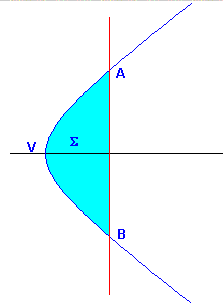
The graph of the transformed curves is like that in the following figure
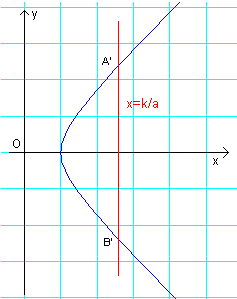
If we draw the segments OA' and OB' we obtain the following figure
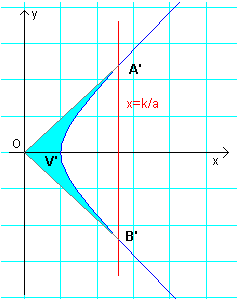
In this figure, the blue colored area is given by the hyperbolic arc cosine of k/a. The area Σ' of the hyperbolic segment A'V'B' can therefore be obtained by the difference between the area of the triangle A'OB' and the hyperbolic arc cosine of k/a.
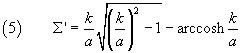
A linear transformation is such that the ratio between the areas of the transformed figures is given by the determinant of the transformation itself, so we have:
![]()
from which
![]()
and finally
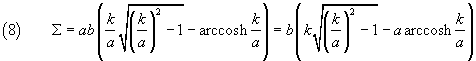
Example.
Given in the cartesian reference frame Oxy the hyperbola with equation
![]() ,
the area of the right hyperbolic segment delimited by the straight line with equation
x=5 is
,
the area of the right hyperbolic segment delimited by the straight line with equation
x=5 is