(notes by Roberto Bigoni)
The ellipse ε with semiaxes a and b (a > 0; b > 0; a ≥ b) in a rectangular planar Cartesian coordinate system Oxy with origin O at its center of symmetry and cartesian axes superimposed on its axes, has equation
![]()
The equation of the arc of ε contained in the first quadrant is
![]()
then
![]()
![]()
![]()
The length dl of an infinitesimal segment of this arc is given by
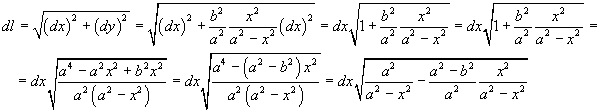
Since
![]()
where e is the eccentricity of ε, we we have
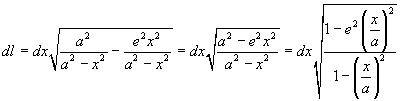
The length q of the arc is given by the integral
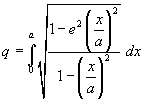
If we let
![]()
we obtain
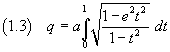
Ultimately, the length of ε is expressed by
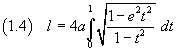
The integral at the right side of (1.3) is said complete elliptic integral of second kind:
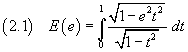
With a further change of variable we can simplify its expression. In fact if we set
![]() we obtain
we obtain
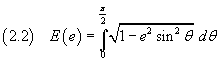
The integrand can be expanded as a power of a binomial
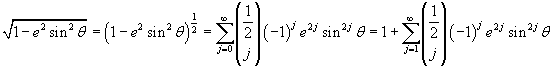
so
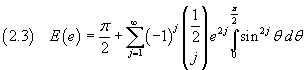
Since for j ≥ 1,
where the double exclamation mark represents the double factorial of its argument, we obtain
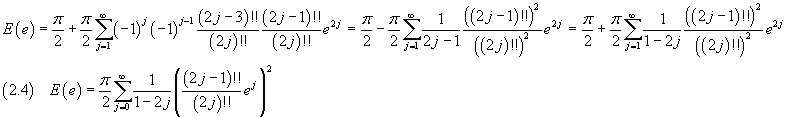
From (1.4) e (2.4) the length of the ellipse with semi-major axis a and eccentricity e is
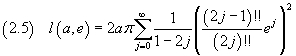
Similarly we can get the series expansion of the integral
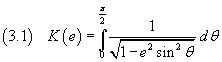
said complete elliptic integral of first kind.
The binomial series expansion of the integrand gives
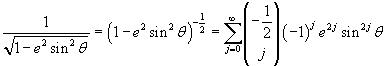
so
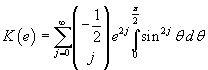
Since
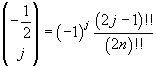
we have
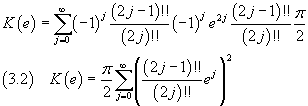
By a Landen's transformation the complete elliptic integral of first kind can be expressed in terms of the arithmetic-geometric_mean
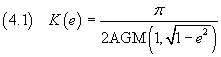
Using this identity we can approximate the value of K(e) with a quite fast and accurate algorithm. Here we show a Javascript code that calculates also E(e). The JavaScript function is derived from a page of A. C. M. de Queiroz.
function ellipticInt()
{
var a, b, a1, b1, amb, E, i, k, kk, IK, IE;
k = parseFloat(document.getElementById("input_e").value);
kk = k*k;
a = 1;
b = Math.sqrt(1-kk);
E = 1-kk/2;
i = 1;
do
{
a1 = (a+b)/2;
b1 = Math.sqrt(a*b);
amb = a-b;
E -= i*amb*amb/4;
i *= 2;
a = a1;
b = b1;
} while (Math.abs(a-b)>1e-15);
IK = Math.PI/(2*a);
IE = E*IK;
document.getElementById("agm").value = a;
document.getElementById("intK").value = IK;
document.getElementById("intE").value = IE;
}
To calculate K(e) and E(e) Mathematica (Wolfram) has the functions EllipticK[m] e EllipticE[m]; due to different notation, the argument m of these functions must be the square of e. Try WolframAlpha.
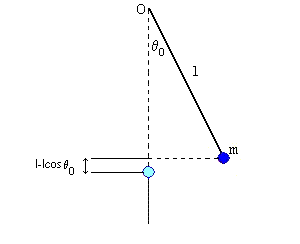
An ideal pendulum is a physical system that consists of a point mass m at one end of an inextensible and massless bar with length l. The bar can rotate without friction around the other end O.
The system is located in a field of constant gravitational acceleration with intensity g and its gravitational potential energy is assumed to be 0 when the mass is vertically below O.
Initially the bar is at rest and forms an angle θ0 with respect to the vertical through O.
and its total energy is
![]()
When the bar is released, the mass begins to fall and θ to diminish. During the fall the potential energy is
![]()
and the kinetic energy is
![]()
Since the mass moves on a circular path
![]()
therefore
![]()
Applying the principle of conservation of mechanical energy we get
![]()
e simplifying
![]()
![]()
From (5.1) we get
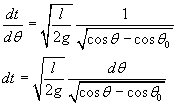
If T is the period of the pendulum, ie the duration of one complete swing, the duration of the descent from θ0 to 0 is
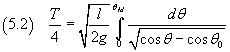
If we set
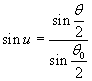
we obtain
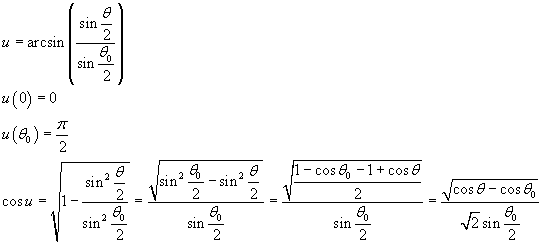
Moreover
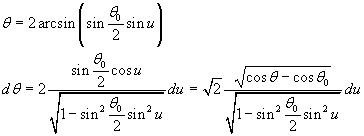
Therefore from (5.2) we have
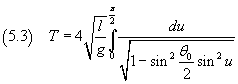
The integral in in (5.3) is a complete elliptic integral of first kind and from (3.2) has value
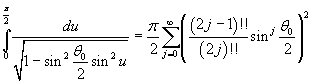
In conclusion, the period of the pendulum is
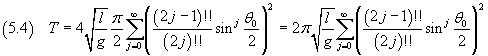
If θ0 is very small, the powers of the sine of its half are physically negligible because they are below the sensitivity of the instruments and the (5.4) simply becomes
![]()
last revision: May 2018