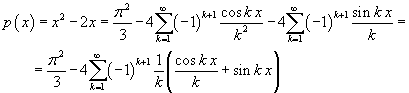In the previous section we have seen that a function φn of the vector space Φn can be expressed by
![]()
The functions φn have the following properties:
If n is a finite number, Φn doesn't include all the possible functions with these properties. We can nevertheless conjecture that the more n increases, the more the set Φn approaches the set Φ of all the periodic functions φ(x), with period 2π, continue, differentiable and having null integral mean value in [-π;π], that is
![]() with
with 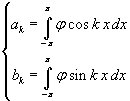
this conjecture can be generalized and extended to the set P of all the real periodic
functions p(x), with period 2π, continue, differentiable and having integral
mean value
![]() so that
so that
![]()
This expression, found by J. Fourier, is commonly said the Fourier series expansion and has been theorically validated by many mathematicians of the 19th and 20th centuries, which have extended its applicability also to less restrictive conditions.
This series expansion can be easily adapted to periodic functions with whatever period 2L
by replacing the x variable with the ξ of the proportion
![]() .
.
If a function p(x) is odd, all the coefficients ak are 0 and one needs to explicitly calculate only the coefficients bk.
Example.
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ; ...
; ...
![]() ;...
;...
![]()
The following JavaScript application allows you to observe that the more the number of harmonics, that is, the number of terms in the summation, increases,
the more the sum approximates the function p(x) = x. It, like the following ones, works only if your browser allows popups.
The abscissas xA and xB are expressed as multiple of π.
If a function p(x) is even, all the coefficients bk are 0 and one needs to explicitly calculate only the coefficients ak.
Example
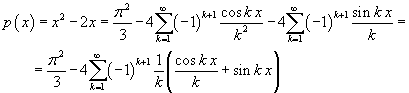
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]() ; ...
; ...
![]()
![]()
The following JavaScript application allows you to observe that the more the number of harmonics, that is, the number of terms in the summation, increases,
the more the sum approximates the function p(x) = x2.
The abscissas xA and xB are expressed as multiple of π.
The expansion of a polynomial is obtained by adding the expansions of its monomials.
Example.