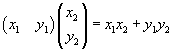
Given the vector v(x;y), the product between v and the real number a is the vector r(ax;ay).
A set of real vectors that can be multiplied by a real number is a real vector space (or linear space). In this context the real number a is said a scalar.
Given two vectors v1(x1;y1) and v2(x2;y2), their scalar (or inner or dot) product v1·v2 is the real number x1x2+y1y2.
The scalar product between the vector v1 and the vector v2 can be represented in the following way
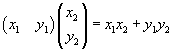
where the vector v1 is written as a row matrix and the vector v2 as a column matrix. The scalar product is given by the sum of the products of the corresponding components of the two vectors.
In these pages we shall sometime use the
bra-ket notation proposed by
P.A.M. Dirac: the row matrix is
a vector bra represented by <w| and the column matrix is a vector
ket represented by |v>. So the scalar product is
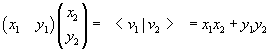
The magnitude of a geometric vector is given by the square root of its square. This quantity is generalized by the norm which usually is the same
![]()
In the scalar product between the vector L1
(L1,1;L1,2)
and the vector v(x;y) in
![]()
![]()
the vector L1 can be interpreted as an operator applied to the vector v to univocally give the real number
![]()
In order to have an univocal correspondence between a vector v(x;y) and a pair of real numbers which could be interpreted as the components of another vector v’(x’;y’), L1 must be joined with another operator L2(L2,1;L2,2) such that
![]()
The ordered pair L of the operators L1 and L2 is represented by a square matrix with two rows and two columns
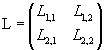
where the Li,j are the entries (or coefficients) of the matrix.
This matrix is called the matrix of the operator L. In general the same capital letter is used to denote an operator and its matrix.
So we have
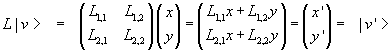
and we can say that applying L to |v> we obtain |v'> or that L transforms |v> in |v'>.
The application of L to |v> can be interpreted as the product of L and |v>, so this product is a vector such that its components are given by the sum of the products of the entries of each row and the corresponding components in the column.
L has the following properties (a is a scalar)
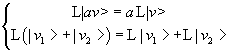
When an operator has such properties (like, for example, the differential operator and the integration operator it is said to be a linear operator.
The operator I having matrix
![]()
when applied to whatever vector gives the vector itself. This operator is the identity operator.