1. The area of a triangle as a function of the coordinates of the vertices.

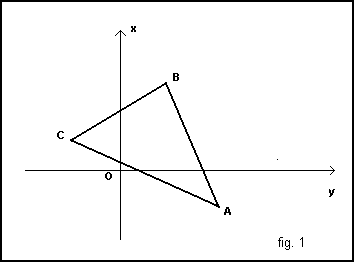
In a Cartesian orthogonal plane Oxy, three non-aligned points, A(x_A;y_A), B(x_B;y_B) and C(x_C;y_C), biunivocally determine the triangle ABC.

In the case in which the three points are arranged as in fig. 1, the problem of calculating the area of the triangle ABC can be solved in the following way:

• we draw the straight line through A parallel to the x axis;
• we draw the straight line through C parallel to the y axis;
• let D be the point of intersection of these lines; the coordinates of D are x_D=x_C and y_D=y_A, then D(x_C;y_A);
• we draw the segment DB.

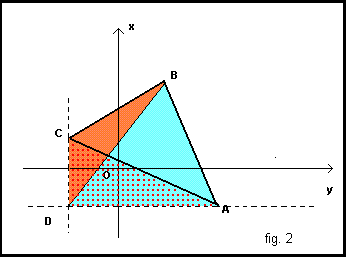
The area of the triangle ABC can be obtained by summing the areas of the triangles DAB and DBC, and subtracting from this sum the area of the triangle DAC

A_ABC=A_DAB+A_DBC-A_DAC

We get

The equation (1.1) produces the correct result if the points A, B, C are sorted counterclockwise. Otherwise the result is negative and we must calculate its absolute value.

The following JavaScript application calculates the solution of the problem.
You can enter the numeric data as integers, fractions, decimals or symbols like E and P or also as values of simple functions (for example Sqrt[2], Sin[1], etc.).
The application works only if your browser allows pop-ups.