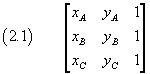
The expression in brackets in (1.1) can be more conveniently written as a third-order determinant, ie a table consisting of three rows and three columns of real numbers
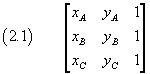
which must be calculated in the following manner, said
Laplacian expansion
The value of a determinant is given by the sum of the products between each element of a row or of a column and its cofactor.
The cofactor of an element aij (i: row index, j: column index) is
the determinant we get if we delete the i-th row and the j-th column,
multiplied by (-1)i+j, ie by 1, if i+j is even, or by -1, if i+j is odd.
As we can see, the Laplacian expansion is recursive, that is, if we want calculate the value of a n-order determinant, we must calculate n n--order determinants. The procedure ends when the cofactors are first-order determinants that is when they contains just a single number.
For example, the above determinant may be expanded in the following way on the elements of the first row:
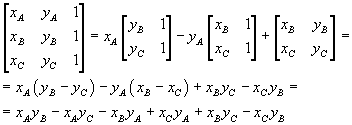
It can be a useful exercise to verify that the same result can be achieved by expanding the determinant on the elements of another row or of another column.
We can therefore conclude that the area of the triangle ABC can be expressed as follows
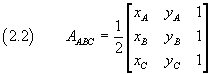
The equation (2.2) was obtained by considering a particular triangle (acute-angled, with vertices in certain quadrants, etc. ..), but we can easily verify that the result can be generalized to any triangle, if we care to order counterclockwise the vertices, and then the rows, of the determinant (2.1).
In fact, the determinants have the following property:
if we swap two lines (or two columns) of a determinant with one another, the determinant changes its sign.
For example, let us expand the following determinant
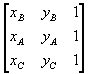
obtained from the determinant (2.1) by swapping the first and the second raw.
From the geometric point of view, the inversion of the two rows corresponds to a clockwise orientation of the vertices.
So we can say that
If the vertices are ordered counterclockwise, the determinant is positive, but if the vertices are ordered in a clockwise direction, the determinant has the same absolute value but negative sign.
Since in Euclidean Geometry, the rotational and linear ordering of the points is not important, and the lengths of the segments and the areas of the figures are only considered in absolute value, we can conclude that the area of a triangle with vertices ABC is given by
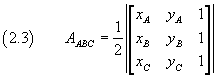
If you know the basics of vector calculus, you can more directly calculate the area of a triangle as a function of the coordinates of its vertices.