3. The equation of the straight line through two points.

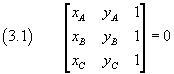
According to what has been said in the previous section, the absolute value of the determinant (2.1) can be geometrically interpreted as twice the area of the triangle with vertices ABC

A(xA;yA), B(xB;yB), C(xC;yC).

Necessary and sufficient condition for A, B and C to be collinear, is that the area of the triangle ABC is zero.

We can therefore say that necessary and sufficient condition for three points A, B, C to be collinear, is that

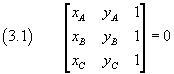
Eqn001.gif

So, if we denote by P(x,y) a generic point of the plane Oxy, P is aligned with two points A(xA;yA), B(xB;yB) if and only if

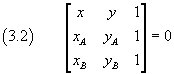
Eqn002.gif

Since the line of the segment AB can be thought of as the locus of the points aligned with A and B, the equation (3.2) can be interpreted as the equation of the straight line through A and B.

If we expand the determinant in (3.2) we get

Eqn003.gif

We can obtain an alternative form of the equation of the straight line through A and B, which is valid only if the segment AB is not parallel to any of the axes, by adding and subtracting to the left hand side of (3.3) the product xByB

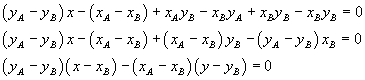
Eqn004.gif

Eqn005.gif

or, as we can see in many textbooks

Eqn006.gif

The following Javascript application allows the calculation of the equation of the straight line through points A and B, given their coordinates;
it also allows the graphical representation of the line.
You can enter the numeric data as integers, fractions, decimals or symbols like E and P or also as values of simple functions (for example Sqrt[2], Sin[1], etc.).
The application works only if your browser allows pop-ups.