If two points A and B have equal ordinate h, the straight line through A and B is parallel to the x-axis.
In this case the equation (3.3) gives
![]()
Conversely we can say that any equation of the form (4.1) represents a straight line parallel to the x-axis.
Similarly, if two points A and B have equal abscissa k, a straight line through A and B is parallel to the y-axis.
In this case the equation (3.3) gives
![]()
Conversely we can say that any equation of the form (4.2) represents a straight line parallel to the y-axis.
In particular, the equations y=0 and x=0 respectively represent the x-axis and the y-axis.
In general, any linear equation in the two variables x and y
![]()
with a, b and c all different from 0, can be interpreted as the equation of the line through the points
![]()
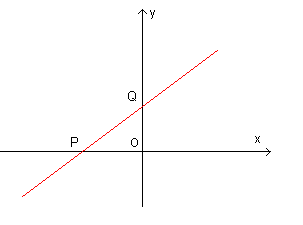
(P and Q lie respectively on the x-axis and the y-axis then the straight line is not parallel to any of the axes)
In fact, if we use the coordinates of P and Q instead of those of A and B in (3.3), we get
![]()
which, simplified, gives the equation (4.3).
We can therefore say that the equation (4.3), with a, b and c all different from 0, is in general the equation of a straight line not parallel to any of the axes.
The equation (4.3) is said implicit form of the equation of a straight line.
From the equation (4.3), if we express y as a function of x, we get
![]()
If we use the coefficients m and q such that
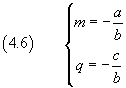
we can write the equation (4.4) as
![]()
This is the explicit form of the equation of a straight line not parallel to the axes (the straight lines parallel to the axes have equations like (4.1) and (4.2)).
The coefficients m and q in the equation (4.6) are said, respectively, slope and intercept.
q coincides with the coordinate of the point Q.
m coincides with the trigonometric tangent of the angle OPQ, ie the angle that the oriented segment PQ forms with the positive direction of the x-axis.
![]()
To check whether a point P belongs to a line we must replace its coordinates xP and yP instead of x and y in the right-hand side of the equation (4.3) and check that the result is 0 or replace its coordinates instead of x and y in the equation (4.7) and check that the two sides of the equation have the same value.
In particular, if the origin O belongs to the line, in (4.3) c must be equal to 0 and, in (4.7), q must be equal to 0.
The following Javascript application allows the graphical representation of the straight line with slope m and intercept q.
You can enter the numeric data as integers, fractions, decimals or symbols like E and P or also as values of simple functions (for example Sqrt[2], Sin[1], etc.).
The application works only if your browser allows pop-ups.