5. Intersection of two straight lines

In the previous sections we we have seen that any equation of the form

represents a straight line in the Cartesian plane Oxy. If a≠0, b≠0, c≠0, the straight line is not parallel to any of the axes; if a=0 and b≠0, the straight line is parallel to the x-axis; if b=0 and a≠0, the straight line is parallel the y-axis.

The equation (5.1) is the equation of a locus, that is, it represents the set of all and only the points P(x,y) whose coordinates verify the equation. A point Q(x_Q;y_Q) belongs to this set if and only if its coordinates x_Q and y_Q, put in place of x and y in (5.1), make the left-hand side of the equation equal to zero.

Let us consider two straight lines r and r'  given by the equations

In Euclidean geometry two straight lines can have only one point in common. The coordinates of this point must simultaneously satisfy the equations of the two lines.

To determine the coordinates of this point is therefore necessary to solve the system formed by the equations of the two lines. There are many ways to solve a system. The most interesting here is the Cramer's rule. We write the system as follows

The solution is

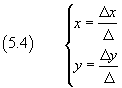
where Δ is the determinant of the coefficients of the variables x e y, Δx is the determinant we obtain from Δ by substituting the first column with the column of the coefficients in the right-hand sides and Δy is the determinant we obtain from Δ by substituting the second column with the column of the coefficients in the right-hand sides:

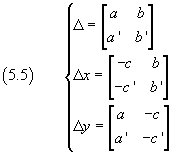
The equation (5.4) highlights the fact that the system has a solution only if the denominators Δ are different from zero.

Otherwise the system

• is impossible if the numerators are nonzero: geometrically this means that the lines are distinct and parallel;
• is indeterminate if the numerators are zero: geometrically this means that the lines are coincident.

We can conclude that: necessary and sufficient condition for two distinct straight lines of equations (5.2) to be parallel, is that the determinant Δ of the coefficients of the variables is equal to 0.

From (5.6) we can deduce that the condition of parallelism between lines can also be stated as follows: necessary and sufficient condition for two distinct lines of equations (5.2) to be parallel, is that the corresponding coefficients of the variables are directly proportional.

Moreover, from (4.6)

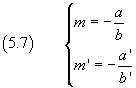
then we can also say that necessary and sufficient condition for two distinct lines to be parallel, is that they have the same slope.

We could achieve the same result more directly by observing that if two straight lines have the same slope, they form, with the positive direction of the x-axis, equal corresponding angles, so they are parallel. The converse is also valid.

The following JavaScript application draws the lines around their point of intersection, if it exists.
You can enter the numeric data as integers, fractions, decimals or symbols like E and P or also as values of simple functions (for example Sqrt[2], Sin[1], etc.).
The application works only if your browser allows pop-ups.