Given in a Cartesian plane Oxy the straight line r: y = mx passing through the origin O, let α be the absolute value of the acute angle it forms with the positive direction of the x-axis; from (4.8) we get
![]()
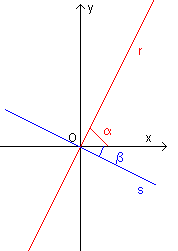
Let s: y = m' x be the perpendicular to r in O and β be the absolute value of the acute angle it forms with the positive direction of the x-axis; let us suppose that, as in the figure above, α is positive so that β is negative. We have
![]()
β is the complementary angle of α, then
![]()
and finally
![]()
If we consider any pair of perpendicular lines, we can draw the parallels to them, with identical slopes, through the origin O.
Therefore, if two lines are perpendicular, their slopes are each the opposite of the reciprocal of the other one.
The inverse statement is valid as well, so necessary and sufficient condition for two lines be perpendicular is that the product of their slopes is equal to -1.
Of course, the above considerations are valid only for lines with slope: please note that the y-axis and the lines parallel to it have no slope.