1. The golden section of a segment and the golden number

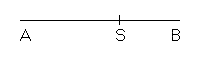
Given a segment AB, its golden section ('the golden cut') is performed by finding a point S so that the segment AS is the mean proportional between AB and SB.

Let λ be the measure of segment AB and σ the measure of segment AS: we have

Solving this equation with respect to σ we get

The segment AS is said the golden portion of segment AB.

The ratio between a segment and its golden portion is said golden number and it is usually denoted by the greek letter Φ.

The reciprocal one of the golden number Φ is denoted by φ.

The relation between σ and λ suggests a way to execute the golden section of a segment AB having length λ using straightedge and compass:

• given the segment AB of measure λ we construct the rectangular triangle the catheti of which are AB and BC, half of AB; the hypotenuse AC has measure
• we trace the circumference Δ of center C and radius CB which intersects the hypotenuse in D.
  The segment AD has measure , which is the measure of the golden portion;
• we trace the circumference Σ of center A and radius AD which intersects the segment AB in S. AS has a measure equal to the one of AD, therefore S is the point which determines the golden section.

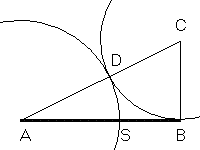
The definition of the golden section implies that the segment SB is in its turn the golden portion of segment AS.

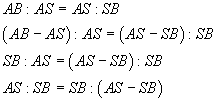
The line perpendicular to segment AB in A intersects Σ in the point E. The rectangle having sides AB e AE is said golden rectangle.

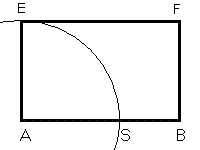
If, conversely, given a segment of measure σ, we want to construct a segment of length λ such that the former be its golden portion, we operate in the following way:

• we draw the segment AB of measure σ, and we build on it an equilateral triangle ABC;

  

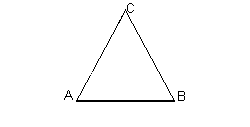
• we double the lengths of the sides CA and CB, obtaining the equilateral triangle DEC;

  

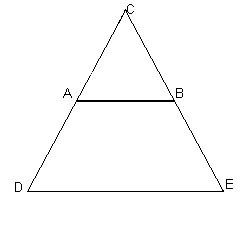
• we draw the circle γ, circumscribed to the triangle DEC;

  

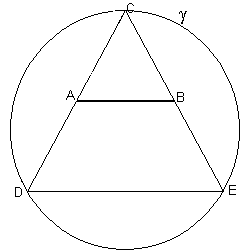
• we prolong the segment AB, until it intersects γ at the points P and Q;

  

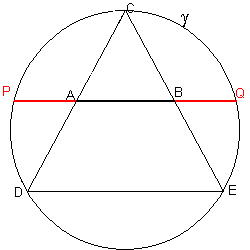
  The segments PB and AQ are such that AB is their golden portion.

Indeed, by the theorem of intersecting chords

and, since

BQ is congruent with PA, which is given by , then

The composition scheme given by the golden rectangle has been very important in the history of western art.