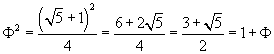
Raising Φ to square we get
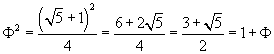
i.e.
![]()
This relation can be interpreted as a recursive definition of Φ. If we replace Φ in the second member with its recursive definition we have
![]()
These substitutions can continue endlessly
![]()
Vice versa, if we add 1 to any initial value ≥-1, and we extract the square root of this sum and again we add 1 and extract the root of the new sum and again we add 1 and extract the root of the new sum and so on, the more we repeat this process, the closer to Φ are the values we get.
Describing synthetically this procedure with proper symbolism, we can write that, given Φ0,
![]()
This expression can be easily implemented in an electronic sheet. As an example, assuming Φ0 = 0, we obtain
0, 1, 1.414213562, 1.553773974, 1.598053182, 1.611847754, 1.616121207, 1.617442799, 1.617851291, 1.617977531, 1.618016542, 1.618028597, 1.618032323, 1.618033474, 1.61803383, 1.61803394, 1.618033974, 1.618033984, 1.618033987, 1.618033988, 1.618033989, 1.618033989, 1.618033989, 1.618033989, 1.618033989, ...
From the equality
![]()
we get also the following recursive definition of Φ
![]()
With a procedure of substitutions analogous to those employed in the previous case we get
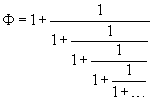
Also in this case, given as initial value of Φ0 any value different from 0, if we calculate its reciprocal value and we add 1 to it and again we calculate the reciprocal value and we add 1 to it and so on, the more times this procedure is repeated, the closer we get to Φ.
So, the expression of Φ as continued fraction id Φ = {1,1,1,1,1,1,1,1,1,1...}.
In mathematical notation we can write that, given Φ0,
![]()
If we assume as starting value of Φ0 an integer number, we obtain a sequence of rational numbers, represented by fractions. As an example, with Φ0 = 1, we have
![]()
This sequence shows interesting regularities:
These properties of this sequence suggest an alternative way to obtain the same sequence.
The sequence of numerators fi is defined by
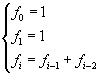
From this definition we can obtain exactly the sequence
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
This sequence is known as the sequence of Fibonacci.
If we calculate the ratios between every number of the Fibonacci sequence and the previous one, we obtain a new sequence of rational numbers converging to Φ.
![]()
The denomination of sequence of Fibonacci comes from the fact that this sequence is described by Leonardo Fibonacci in his Liber Abaci of 1202, with the proposition of a curious issue on the proliferation of the rabbits.
| Liber Abaci | translation |
|---|---|
| Quot paria coniculorum in uno anno ex uno pario germinentur. | How many pairs of rabbits come in a year from one pair. |
| Qvidam posuit unum par cuniculorum in quodam loco, qui erat undique pariete circundatus, ut sciret, quot ex eo paria germinarentur in uno anno: cum natura eorum sit per singulum mensem aliud par germinare; et in secundo mense ab eorum natiuitate germinant. | A man put one pair of rabbits in a place completely encircled by a wall, in order to discover how many pairs of rabbits came from this pair in a year: by nature the pairs of rabbits generate another pair after a month, and begin to breed from the second month from their birth. |
| Quia suprascriptum par in primo mense germinat, duplicabis ipsum, erunt paria duo in uno mense. |
Since the aforesaid pair breeds in the first month, we must double it: in the first month the pairs are therefore two. |
| Ex quibus unum, scilicet primum, in secundo mense geminat; et sic sunt in secundo mense paria 3; | In the second month, the first of these two pairs generates another pair: therefore in the second month there are 3 pairs. |
| ex quibus in uno mense duo pregnantur; et geminantur in tercio mense paria 2 coniculorum; et sic sunt paria 5 in ipso mense; | During the month, two of these begin to be pregnant and, in the beginning of the third month, they generate 2 pairs of rabbits: therefore, in the third month, there are 5 pairs of rabbits. |
| ex quibus in ipso pregnantur paria 3; et sunt in quarto mense paria 8; | 3 of these, during the month, begin to be pregnant and in the fourth month there are 8 pairs. |
| ex quibus paria 5 geminant alia paria 5: quibus additis cum parijs 8, faciunt paria 13 in quinto mense; | In the fifth month, 5 pairs of these generate other 5, which, added to the 8 existing pairs, make 13 pairs. |
| ex quibus paria 5, que geminata fuerunt in ipso mense, non concipiunt in ipso mense, sed alia 8 paria pregnantur; et sic sunt in sexto mense paria 21; | The 5 last born of these do not conceive during the month, but the other 8 become pregnant, therefore in the sixth month there are 21 pairs. |
| cum quibus additis parijs 13, que geminantur in septimo, erunt in ipso paria 34; | Adding to these the other 13 pairs born in the seventh month, there will be 34 pairs in that month. |
| cum quibus additis parijs 21, que geminantur in octauo mense, erunt in ipso paria 55; | Adding to these the other 21 pairs born in the eighth month, there will be 55 pairs in that month. |
| cum quibus additis parijs 34, que geminantur in nono mense, erunt in ipso paria 89; | Adding to these the others 34 pairs born in the ninth month, there will be 89 pairs in that month. |
| cum quibus additis rursum parijs 55, que geminantur in decimo mense 144; | Newly adding to these the other 55 pairs born in the tenth one, there will be 144 pairs. |
| cum quibus additis rursum parijs 89, que geminantur in undecimo mense, erunt in ipso paria 233. | Newly adding to these the other 89 pairs born in the eleventh month, there will be 233 pairs in that month. |
| Cum quibus etiam additis parijs 144, que geminantur in ultimo mense, erunt paria 377; | Newly adding to these the 144 pairs born in the last month, there will be 377 pairs. |
| et tot paria peperit suprascriptum par in prefato loco in capite unius anni. | This is the number of pairs generated by the aforewritten pair in that place during one year. |
| Potes enim uidere in hac margine, qualiter hoc operati fuimus, scilicet quod iunximus primum numerum cum secundo, uidelicet 1 cum 2; et secundum cum tercio; et tercium cum quarto; et quartum cum quinto, et sic deinceps, donec iunximus decimum cum undecimo, uidelicet 144 cum 233; et habuimus suprascriptorum cuniculorum summam, uidelicet 377; et sic posses facere per ordinem de infinitis numeris mensibus. | You can moreover see here on the side how we have operated: we have added the first number with the second one, that is 1 and 2; the second one with the third one, the third one with the fourth one, the fourth one with the fifth one and so on until we have added the tenth one with the eleventh one, that is 144 with 233 and we have obtained the sum of the aforesaid pairs of rabbits, that is 377 and therefore it can be made infinitely for a number of months. |
The sequence of Fibonacci was known to the ancient Indian mathematicians Virahanka and Gopala (1133). Very probably these mathematicians, like also Hemachandra and Pandita, continued a more ancient tradition started by Pingala (200 a.C.), which in his analysis of the poetic meter of Indian poems, found the numeric triangle (the Mount Meru) that we now call Pascal Triangle and, whithin it, the Fibonacci's numbers.
In fact, starting from the first number of each row and adding together all the numbers in the diagonal SW-NE, we obtain the Fibonacci's numbers.
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | |
| 1 | |||||||||||
| 1 | 1 | ||||||||||
| 1 | 2 | 1 | |||||||||
| 1 | 3 | 3 | 1 | ||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||
| 1 | 5 | 10 | 10 | 5 | 1 | ||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | |||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | ||||
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | |||
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | ||
| 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 101 | 1 |
The most common mathematical packages have a specific function for the calculation of Fibonacci numbers.
For example Mathematica by Wolfram has the function Fibonacci[n] that can be used directly or in more complex contexts.
The figure below provides an example of calculation of the first 20 Fibonacci numbers with WolframAlpha, which is an app that can understand
the statemants of Mathematica.
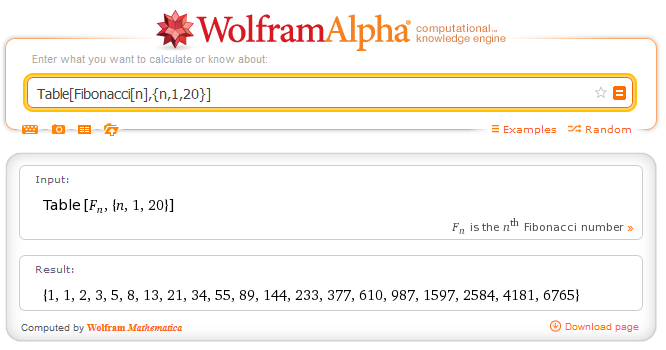
Try Fibonacci with Wolfram Alpha
If we need such function in our own application, the idea of apply a recursive algorithm is very unhappy, because of the exponential explosion of the time of calculation: to obtain the nth number, two foregoing numbers must be calculated; for each of them, other two foregoing numbers and so on.
Therefore, for example, the following Javascript function is maybe mathematically elegant, but surely inefficient.
function fibonacci(n)
{
if ((n==0)||(n==1)) return 1;
else return fibonacci(n-1)+fibonacci(n-2);
}
An iterative algorithm is much better. For example, this Javascript function works fine for integer arguments less than 79.
function fibonacci(n)
{
if (n<3) return 1;
else
{
var result, i, prec=1, precprec=1;
for (i=3; i≤n; i++)
{
result = precprec+prec;
precprec = prec;
prec = result
}
return result;
}
}
This function is used in the following form (do not use indexes greater than 78).
More advanced programming methods, such as creating a JavaScript object that can represent and process natural numbers still large, can calculate exactly very large Fibonacci numbers (but the computation time can become prohibitively expensive). For example, you can write JavaScript applications such as the following.
It is possible to calculate directly the nth Fibonacci's number from a linear combination of the nth powers of Φ and -φ. Infact, if we let
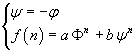
with the conditions
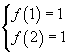
we obtain
![]()
therefore
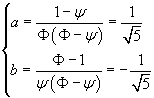
At the end
![]()
The function f(n), commonly attributed to J. Binet but found before in A. De Moivre and in L. Euler, for integer n, calculates directly Fibonacci's numbers. Infact
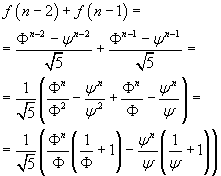
But
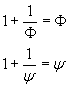
so we have
![]()
Using the Binet's function, the calculation of the nth Fibonacci's number can be implemented, in Javascript, in the following way
function fibBinet(n)
{
var n = parseInt(n);
if (isNaN(n))
{
alert("Write a number, please.");
return 0;
}
if (n>70)
{
alert("Index out of range.");
return 0;
}
with (Math)
{
var rad5 = sqrt(5);
var Phi=(rad5+1)/2;
var psi=(1-rad5)/2;
return round((pow(Phi,n)-pow(psi,n))/rad5);
}
}
Other algorithms and other languages can be found in Wikipedia