Counting partitions

1. Partition of a set

A finite set S with n elements can be subdivided into k parts p_i such that

∀i, p_i ≠ ∅
h ≠ k ⇒ p_h ∩ p_k = ∅

Each of these possible subdivisions is said a partition of S.

2. Stirling numbers of the second kind

If the elements of S are all distinguishable, the number of its partitions in k parts (or k-partitions) is represented by the symbol , proposed by the Serbian mathematician Jovan Karamata in analogy with the symbol used for the binomial coefficients, id said Stirling number of the second kind, named after the Scottish mathematician J. Stirling

Given n, the following identities are immediate:

because there is only one way to split S in only one part;
because there is only one way to split S in n singletons; a singleton is a set with only one element;
In fact, let s be any element of S and C_s the complementary set of the singleton {s} with respect to S; the number of all possible non-empty subsets Σ_i of C_s is 2^n-1-1; each Σ_i identifies a bipartition of S given by Σ_i and its complementary with respect to S.
In fact, in this case the number of partitions coincides with the number of the different pairs of elements of S; a partition formed by a pair and by the singletons of the remaining n-2 elements is a partition into n-1 parts.
One gets immediately the following values:

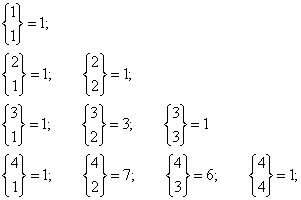
If n > 1 and s is one of the elements of S, the k-partitions of S may be of two kinds:

those which contain the singleton {s}: we call such partitions of kind X;
those which do not contain the singleton {s}: we call such partitions of kind Y.

Let C be the complementary of {s} with respect to S.

The partitions of kind X are because every (k-1)-partition of C united with the singleton {s} forms a k-partition of S.

The partitions of kind Y are , because every k-partition of C united with the singleton {s} forms a k-partition of S.

Assuming

one gets

For n>1, the equation (1,1) allows to derive recursively the Stirling numbers of the second kind.

If n=5:

The following Javascript application allows to calculate the Stirling numbers of the second kind (big numbers may require a lot of computing time).

For big numbers you can use WolframAlpha.

Writing the Stirling numbers in successive rows with increasing n and k, we get the triangle of Stirling.

2. Grunert's polynomials

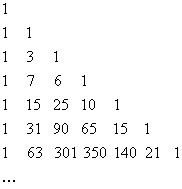
We can directly obtain the values of using the Grunert's polynomials. Given a continuous function f(x), we define the operator G such that

If f(x)=e^x, we have

Successive applications of G to the results of the previous applications give

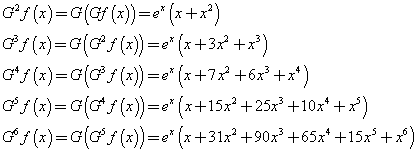
The polynomials that multiply the exponential function are the Grunert's polynomials.

We observe that the coefficients of the Grunert's polynomials coincide with the Stirling numbers of the second kind. This is not accidental because they are formed in the same recursive way. In fact, if we represent with gⁿ_k the coefficients of the polynomial of Gⁿ, we have

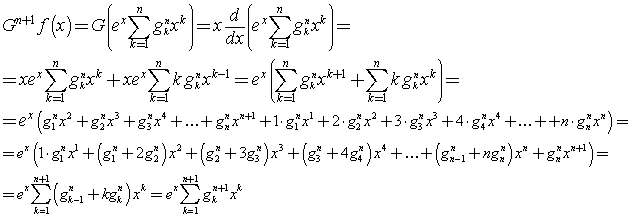
then

The formation of the coefficients g_n,k coincides with the equation (1.1), then

If now we repeatedly apply the operator G to the expansion in Maclaurin series of the natural exponential function we get

By equating the two expressions of Gⁿ, we get

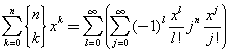
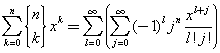
The sum at the right side is a sum on the growing powers of x with exponents l+j. Since the sum at the left side if finite, with k from 0 to n, we assume

then

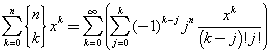
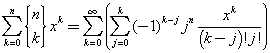
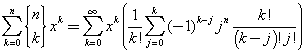
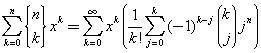
By comparing the sums at both sides, we get

This equation connects the Stirling numbers of the second kind with the binomial coefficients and allows a faster calculation.

Since , from (1.2) we get

By multiplying both the sides of (1.3) by (-1)ⁿ

The power (-1)^2n-j are identical to powers (-1)^j, then

To know more

3. Bell numbers

If the n elements of S are all distinguishable, the number of its partitions is given by the sum of all the Stirling numbers of the second kind with k from 1 to n. This number is known as Bell number B_n, named after the mathematician and novelist E. T. Bell.

The Bell numbers can be recursively obtained with the following procedure

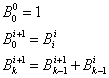
that is

the only number in the first row is 1
in any new row:
- the number in the first column is the last number of the previous row;
- the numbers in the other columns are the sum of the number in the leftmost column with the number above this number in the previous row.

In this way we can build the Bell triangle.

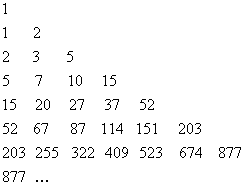
The numbers in the first column are the Bell numbers.

The following Javascript application allows to obtain the Bell numbers (big numbers may require a lot of computing time).

For big numbers you can use WolframAlpha®.

4. Partition function

If the n elements of a set S are all indistinguishable from one another, the number of its partitions is drastically reduced compared to that calculated by the Bell number.

In fact, if, for example, we consider the set I = {a,b,c,d}, the number of its partitions is B₄ = 15, but if we consider the set S = {a,a,a,a}, we can extract from it the following partitions:

{a}, {a}, {a}, {a}
{a}, {a}, {a, a}
{a, a}, {a, a}
{a}, {a, a, a}
{a, a, a, a}

then the number of its partitions is 5.

The calculation of the number of partitions of a set of n indistinguishable elements coincides with the calculation of the number of ways in which the natural number n can be written as a sum of positive natural summands ≤ n. So the term partition can be imported from set theory to that of the natural numbers.

Given a positive natural number n, we call partition Λ_n,k of n a non-decreasing sequence of positive natural numbers λ_n,i ≤ n

such that

Obviously, the maximum value of k, that is, n, is obtained in the case in which all the λ_n,i are equal to 1.

It is obvious that the number 1 admits only the partition .

The number 2 admits two partitions:

The number 3 admits three partitions:

The number 4 admits five partitions:

The number 5 admits seven partitions::

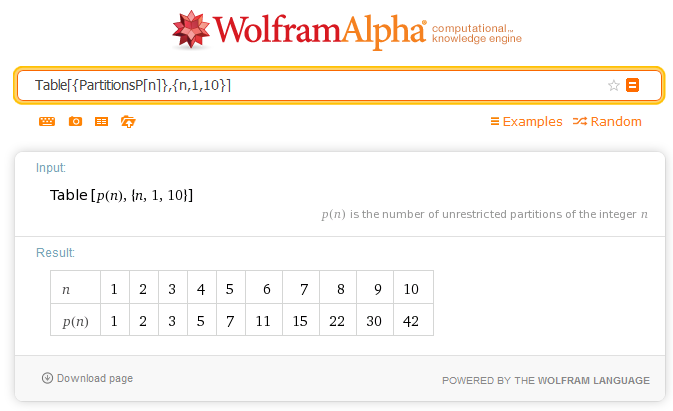
Given any positive natural number n, the number p(n) of its possible partitions is given by the partition function.

From the proposed examples we get

p(1)=1
p(2)=2
p(3)=3
p(4)=5
p(5)=7

5. Partition function and pentagonal numbers

As we can see in the bibliography of the cited page of Mathworld, several mathematicians have studied the properties of the partition function, in particular with the aim of identifying algorithms that allow the determination of its value for any argument n.

A first important result was the recursive formula of Euler, for which the values of p(n) are given by the values p(n_i ) of all the numbers that are obtained by subtracting from n the generalized pentagonal numbers ω_i≤n. We assume p(0)=1.

The set Ω of generalized pentagonal numbers ω_i is obtained from the union of sequences of natural numbers defined as follows

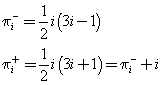
If, for example, n=10, the numbers n_i obtained by subtracting 10 from the generalized pentagonal numbers ω_i ≤10 are:

n₀=10-ω₀=10
n₁=10-ω₁=9
n₂=10-ω₂=8
n₃=10-ω₃=5
n₄=10-ω₄=3

The Euler's recursive formula states that, given the maximum index i_M for the numbers n_i

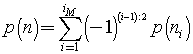
where (i-1):2 represents the integer quotient of i-1 divided by 2.

In practice, in the sum two positive terms alternate with two negative terms.

Euler's formula is recursive because the calculation of p(n) is possible only after the calculation of all the values p(n_i ) which, in turn, can be obtained with the same formula.

Taking the previous example

p(10) = p(9) + p(8) - p(5) - p(3)

Then we must calculate p(9), p(8), p(5) e p(3)

By the Euler's formula

p(9) = p(8) + p(7) - p(4) - p(2)
p(8) = p(7) + p(6) - p(3) - p(1)
p(5) = p(4) + p(3) - p(0)
p(3) = p(2) + p(1)

To calculate p(10) we must know all the values from p(0) to p(9).

In general, to calculate p(n) we must first calculate all the values from p(0) to p(n-1).

The number of these values coincides with the number of the generalized pentagonal numbers ≤ n.

The following Javascript application allows to obtain the values of p(n) (big numbers may require a lot of computing time).

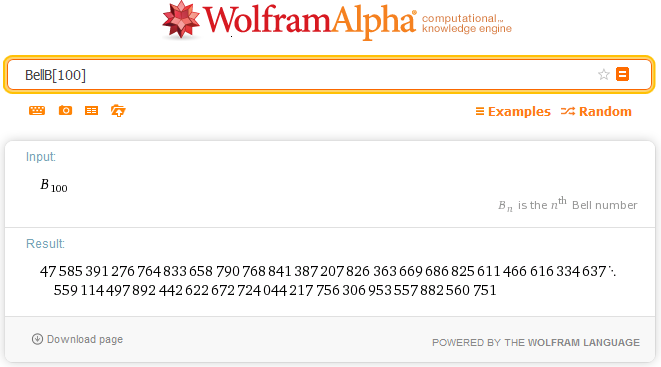
As we can see from the picture, p(n) increases rapidly as n increases. For example, p(1000)=24061467864032622473692149727991. This value is given by WolframAlpha®, where the value of p(n) is produced by the function PartitionsP[n] of Mathematica® and where you can change the value of the argument.

For very large values of n many mathematicians have developed increasingly efficient algorithms. For example, Mathematica® applies the method of Hardy- Ramanujan- Rademacher. Recently the mathematician Ken Ono has provided new important contributions.

last revision: May 2016