The analogy between the golden number Φ and the plastic number P led mathematicians to investigate whether even for P it was possible to define a sequence analogous to that of Fibonacci, ie a sequence of natural numbers from which to extract a sequence of fractions converging to P.
A first solution to the problem, proposed by R. Perrin and therefore known as the Perrin sequence, can be found in the following way.
Let α, β and γ, where α is real and β e γ complex conjugates with norm < 1, be the roots of the equation
![]()
that is numbers such that
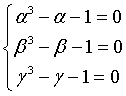
and let pi be the sum of their powers with exponent i
![]()
you immediately have p0 = 3.
Moreover
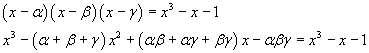
Since the polynomials must be identical, you have
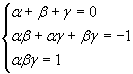
The sum of the first powers of the roots is equal to 0, so p1 = 0.
The sum of the squares of the roots can be obtained in the following way
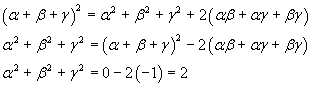
The sum of the squares of the roots is equal to 2, so p2 = 2.
The sum of the cubes of the roots can be obtained in the following way
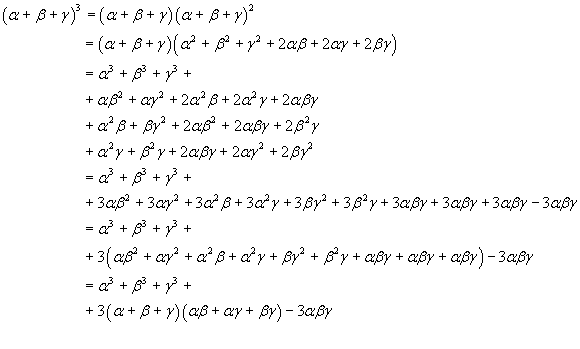
You have
![]()
and, since the sum of the roots is 0 and their product is 1,
![]()
The sum of the cibes of the roots is 3, so p3 = 3.
Moreover you can observe that
![]()
that is
![]()
because the sum of the powers of α is
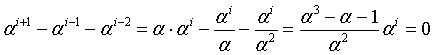
and the same holds for the sums of the powers of β and γ.
Therefore, given p0, p1, p2 and p3, you can obtain all the terms pi of the sequence
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ... |
| pi | 3 | 0 | 2 | 3 | 2 | 5 | 5 | 7 | 10 | 12 | 17 | 22 | 29 | 39 | 51 | 68 | 90 | 119 | 158 | 209 | 277 | ... |
This is the Perrin sequence; its terms are the Perrin numbers.
The use of the recursive definition for the computer calculation of the n-th Perrin is impractical. Better to use a loop, as in the following Javascript implementation
function nPerrin(n)
{
n = parseInt(n);
var n1, n2, n3, p;
switch(n)
{
case 0: return 3;
case 1: return 0;
case 2: return 2;
default:
n1 = 2;
n2 = 0;
n3 = 3;
for (var i=3; i <= n; i++)
{
p = ( n2 + n3 );
n3 = n2;
n2 = n1;
n1 = p;
}
return(p);
}
}
If you can use Mathematica (Wolfram), you may define the following function
PerrinN[n_]:=Switch[n,0,3,1,0,2,2,_,Module[{i,n1,n2,n3,val},n1=2;n2=0;n3=3;
For[i=3,i <= n,i++,val=n2+n3;n3=n2;n2=n1;n1=val];val]]
Table[PerrinN[n],{n,0,30}]
{3,0,2,3,2,5,5,7,10,12,17,22,29,39,51,68,90,119,158,209,277,367,486,644,853,1130,1497,1983,2627,3480,4610}
The Perrin sequence, as it was proposed, has the following property.
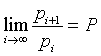
Infact, if α is the real root, that is P, and β and γ are conjugate complex numbers with norm < 1, their powers converge to 0 as the exponent increases. So
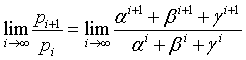
By dividing numerator and denominator by αi
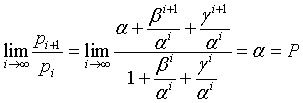
The French mathematician E. Lucas noticed an interesting property of the Perrin numbers analyzed by him: if the index i of a termn pi of the sequence is prime, the term is exact multiple of the index. For example
| pi | 3 | 0 | 2 | 3 | 2 | 5 | 5 | 7 | 10 | 12 | 17 | 22 | 29 | 39 | 51 | 68 | 90 | 119 | 158 | 209 | 277 | ... |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ... |
| resto | 0 | 0 | 0 | 2 | 0 | 5 | 0 | 2 | 3 | 7 | 0 | 5 | 0 | 9 | 8 | 10 | 0 | 14 | 0 | 17 | ... |
Theorem: If i is prime, i is a divisor of pi.
If i is a prime number, you have
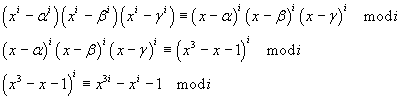
Therefore, for the transitivity of the congruence modulo i you have
![]()
Moreover you have
![]()
The coefficients of x2i must b equal, so
![]()
that is
![]()
Thus, if i is prime, the i-th number of Perrin is divisible by i.
But this does not imply the inverse theorem: you cannot say that if the n-th Perrin number is divisible by n then n is prime.
If the inverse theorem were valid, it would offer a valid primality test: to know if a number is prime you check whether it is an exact divisor of the corresponding Perrin number.
But this conjecture has been falsified: there are numbers divisible by the corresponding index which are not prime: these numbers are called
Perrin pseudoprimes.
For example, p271441 is divisible by 271441, but 271441 is not prime: it is the square of 521; 271441 is therefore a Perrin pseudoprime.
(The calculation of p271441 can be performed by the proposed JS application but may take a few minutes; if possible, try Mathematica.)