4. The Padovan sequence.

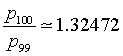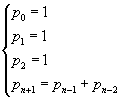
The search for a sequence of natural numbers such that the ratio between each of them and the previous one converges to the plastic number was also made by the architect Richard Padovan who discovered that the sequence p_n generated by

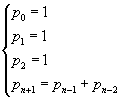
has the same behavior as the Perrin sequence. This sequence is said Padovan sequence and its terms Padovan numbers.

Padovan numbers p_i can be deduced as follows.

1. Let p_i bi a linear combination of the i-th powers of the roots α, β and γ of the equation x³-x-1 = 0, where α is real and β and γ conjugate complex numbers with absolute value < 1:
   
2. Let p₀, p₁ and p₂ be equal to 1: you have
   
3. The solution of the system is
   
4. so
   

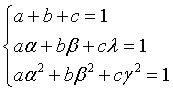
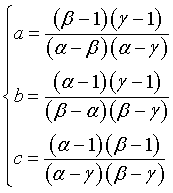
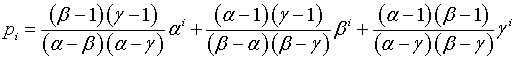
This definition of p_i implies

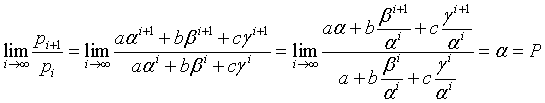
because as the exponent approaches the infinity, the powers of β and γ converge to 0.

Moreover you have

that is

Infact

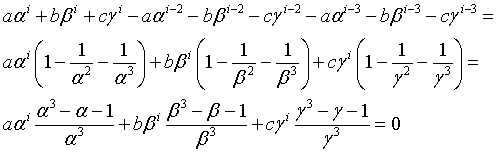
The use of the recursive definition for the computer calculation of the n-th Padovan number is impractical. Better to use a loop, as in the following Javascript implementation

function nPadovan(n)
{
  n = parseInt(n);
  if (n < 2) return 1;
  var n1 = 1;
  var n2 = 1;
  var n3 = 1;
  var p;
  for (var i=3; i<=n; i++)
    {
      p = n2 + n3;
      n3 = n2;
      n2 = n1;
      n1 = p;
    }
  return(p);
}

If you can use Mathematica (Wolfram), you may define the following function

PadovanN[n_]:=Switch[n,0,1,1,1,2,1,_,Module[{i,n1,n2,n3,val},n1=1;n2=1;n3=1;
      For[i=3,i <= n,i++,val=n2+n3;n3=n2;n2=n1;n1=val];val]]
 Table[PadovanN[n],{n,0,30}]
 {1,1,1,2,2,3,4,5,7,9,12,16,21,28,37,49,65,86,114,151,200,265,351,465,616,816,1081,1432,1897,2513,3329}

In general, any sequence of numbers q_i expressed as a linear combination with coefficients a, b, c of the i-th powers of the roots α, β and γ, given three arbitrary values for q₀ , q₁ and q₂, shows the same recursion and the ratio between each term and the previous one converges to P.

For example, the sequence

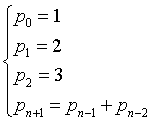
that is

is such that