3. Discrete probability distributions

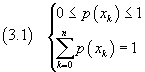
If the sample space is the ordered set of the n discrete real values x_k that can can be taken by the real variable x, a real function p(x_k) such that

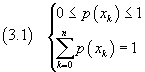
is said a discrete probability distribution and x is said a random or stochastic variable.

For simplicity's sake, in this section we let

then

Mean and variance

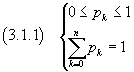
Given a discrete probability distribution, two most important descriptors of its global properties are the mean (or expected value) and the variance.

The mean is given by

If we write as ξ_k the deviation of the value x_k from the mean,

the variance, written as σ² is the mean of the squares of the deviations:

The square root of the variance is said standard deviation of the population:

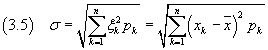
The standard deviation is important because it gives an evaluation of the spread of the values x_k around the mean: the bigger σ the bigger is the dispersion.

Theorem: The variance is the difference between the mean of the squares and the square of the mean.

Proof

Discrete uniform distribution

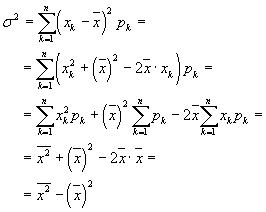
When the n values p_k are all equal the distribution is said uniform.

From the second of the equalities (3.1) we get

In particular, if x_k=k, the mean is

We have applied the equality

known from the theory of arithmetic progressions.

From the equality (3.6), the variance is

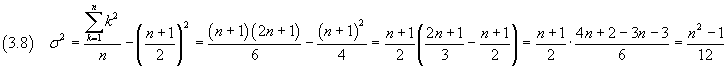
We have applied the equality

obtained by induction.

The standard deviation is

Example

In a roll of a fair dice each of the six outcomes k has probability .

The mean value is

The variance is

and the standard deviation

Discrete binomial distribution (Bernoulli distribution)

Given the number of trials n and the probability p, the function p_k=P_n,k in the equality (2.9) represents the probability distribution of the random variable k that can take integer values from 0 to n because this function satisfies the conditions (3.1.1). In fact, since p+q=1 by hypothesis,

Such probability distribution is said binomial distribution or Bernoulli distribution.

From the equality (3.2) the mean value of the binomial random variable k over n trials is

If we expand the right side we have

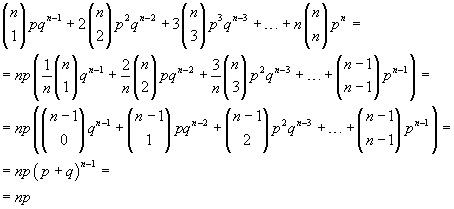
and finally we get

Moreover we have

The expansion of the right side gives

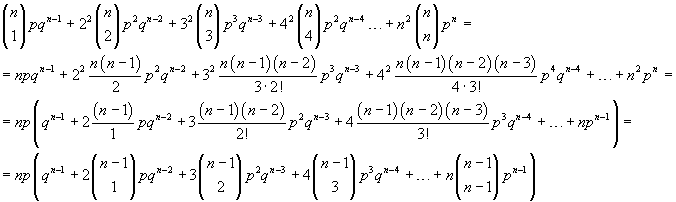
The expression in brackets can be divided into two sums

s₂ is the mean value of the binomial random variable k over n-1 trials, so from (3.10),

Then we get

and finally

The following JavaScript application allows you to calculate and to graph a binomial distribution. The probability p can be expressed either as a decimal or as a fraction. The values on the ordinate are expressed as a percentage. To view the tables, your browser must allow popups.
If your browser does not allow internal frames, you can directly access the application page.

Poisson distribution

As p approaches 0 and n approaches infinity, the binomial distribution converges to the Poisson distribution.

In this case, if λ represents the mean value of the distribution, we have

The equality (3.14) may be obtained in the following way:

From (2.9) we have
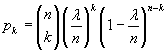
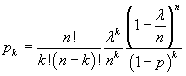
If n→∞ and p→0

then

If p→0, q→1, then, from the equality (3.12),

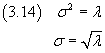
The following JS application calculates the probability that an event will occur k times in a Poisson distribution of a fixed mean λ
If your browser does not allow internal frames, you can directly access the application page.

The following JavaScript application allows you to calculate and to graph a Poisson distribution. The values on the ordinate are expressed as a percentage. To view the tables, your browser must allow popups.
If your browser does not allow internal frames, you can directly access the application page.