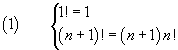
The factorial n! of a natural number is recursively defined as
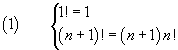
L. Euler found that it is possible to define a function of a real (or complex) variable Γ(x) ('Gamma of x') with the same recursive property
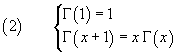
If we apply such function to an argument x+1 coincident with a natural number, we have
So Γ, for natural arguments, produces values identical to those of the factorial
Euler was able to express the function Γ in this way:
In fact the definition (4) gives
and also
In particular, if x coincides with the natural number n, we can write the following equalities
Using the second one of the equalities (2), given
, we can calculate the values
for each natural number
n ≥ 1.
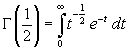
With t=z2, we have
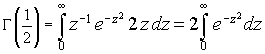
The last integral is a well known
gaussian integral and has value
. Therefore
The values of Γ for subsequent increments by 1 of the argument can be obtained recursively
In general, for n ≥ 0,
In the equality (8) the double question mark represents the double factorial of the natural number before it, that is, if the number is odd, the product of the number itself by all the preceding odd numbers, and, if the number is even, the product of the number itself by all the preceding even numbers. Moreover we assume -1!! = 0!! = 1
The equalities (7) e (8) allow to extend the definition of the factorial from the set of the natural numbers
to the set
in the following way
In particular
From the second one of the equalities (2) we have also
therefore
and recursively
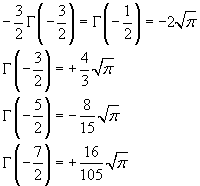
In general, for n ≥ 0,
We can therefore define the values of the factorials also on the set
in the following way
In particular
The following Javascript application allows you to approximate the values of Γ(x) for real or complex arguments.
If your browser does not allow the iframe tag, you can directly open its page.
In the input field you can use the decimal digits, the constants P for π,
E for the exponential notations and I for the imaginary unit.
The definition of the double factorial of a natural number, in a similar way as for the factorial, implies the following recursive relation
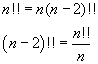
if we use these relations for numbers less than 1, we obtain
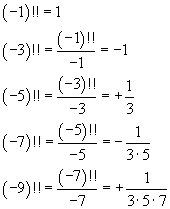
In general, for n ≥ 1,
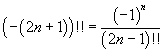
Therefore it is possible to calculate the double factorial of a negative integer if it is odd. But this calculation is not possible for a negative integer if it is even because the calculation of (-2)!! implies the division by 0.
The equality (11) allows us to calculate
binomial coefficient like
.
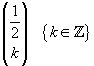In fact, if we express binomial coefficients in terms of factorials, we have
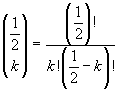
If k=0, we have immediately
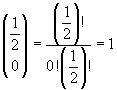
and, for k≥1
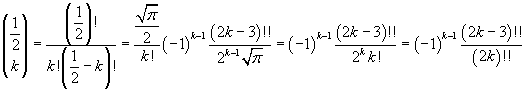
In particular:
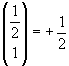
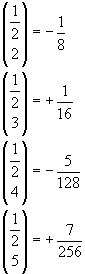
If we now compare this sequence with the sequence of the coefficients of the powers of the variable x in the Maclaurin series expansion of the square root of (1-x) (for x real and ≤1)
we see that these series coincide. Therefore we can write
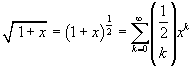
This identity allows us to apply something like the binomial theorem also when the exponent of the binomial isn't a natural number.
But we can do the same if, instead of
, the first term of the
binomial coefficient is any real number r. In fact, given
G = Γ(r), we have
and also
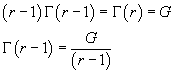
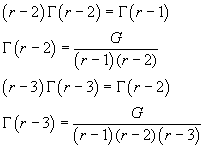
In general, for n natural ≥ 1,
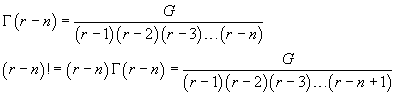
Finally
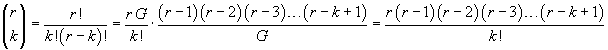
and, more synthetically,
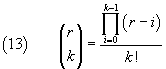
Examples.
Negative integers.
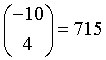
Rational numbers.
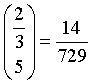
Real numbers.
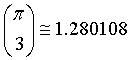
Complex numbers.
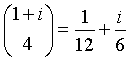
The equation (13) allows us to obtain the series expansion of many functions avoiding the laborious derivations needed by the method of Maclaurin.
The following Javascript application allows you to approximate the values of the binomial coefficients for real or complex arguments.
If your browser does not allow the iframe tag, you can directly open its page.
In the input field you can use the decimal digits, the constants P for π,
E for the exponential notations and I for the imaginary unit.
If in the integral in the identity (7) we let
we obtain
that is
If we now multiply and divide the integrand function by en and extract from the integral the factors that does not depend on the integration variable y, we have
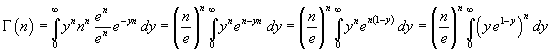
The derivative of the integrand function
with respect to y is
therefore f(y) has an absolute maximum for y=1. In order to approximate the integral, we may express it as a function of w = y-1
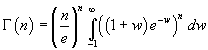
and then approximate the integrand function f(w) in the following way (see MathWorld):
we calculate the logarithm of the function
if n is large enough, the function approaches quickly to 0 on the left and on the right of the maximizing argument, so we can assume the absolute value of w near to 0; for w such that |w|<1 we can expand the logarithm using the Mercator's series
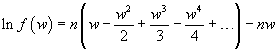
and therefore
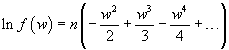
If we truncate the expansion at the first order term, we have
that is
Now we have
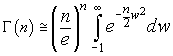
Since by hypothesis the function f(w) goes quickly to 0 in a neighbourhood of 1, the value of this integral does not change appreciably if we extend the limits from -∞ to +∞
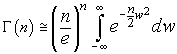
The integral in the right side is a
Gaussian integral
and has value
;
therefore we have
and finally
The formula (14) is the Stirling's approximation to n! and is very useful in several probabilistic and statistical calculations.
For example:
for 10! instead of the correct value 3628800 it gives 3598697; the error is 8 ‰;
for 100! the error is 0.8 ‰;
for 1000! the error is 0.08 ‰.
It is often useful to calculate the logarithm of the factorial. From (15) we have
For large n the last term is negligible and we can simply write
The following Javascript application allows you to compare the exact value of the factorial of a natural number
with that obtained with the Stirling's approximation.
If your browser does not allow the iframe tag, you can directly open its page.
