If we apply a vector a to the origin O of an orthogonal cartesian reference frame Oxyz and we project a on the coordinate axes, we'll obtain three vectors such that, conversely, their sum gives a. These three vectors are the cartesian components of a.
Since the point at the head of the vector bijectively corresponds to a triple of real numbers, that is the ordered set of its cartesian coordinates, each component is given by the product of the versor of the correspondent axis by the correspondent cartesian coordinate.
Let i, j, k be the axes' versors and ax, ay, az the cartesian coordinates of the head of the vector a. Then we have
![]()
If we sum the six cartesian components of the vectors a e b and pick out the versors as common factors, we'll obtain
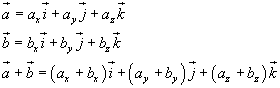
The opposite of the vector b has components
![]()
so the difference a-b is given by
![]()
Given the cartesian components of the the vectors a e b and their cross product
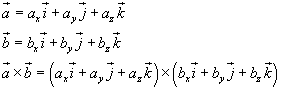
if we apply the distributive law, we'll obtain
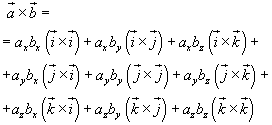
The cross product of a vector by itself is null, so the product can be simplified:
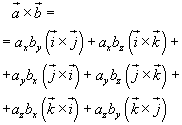
Furthermore we know that
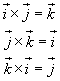
and that if we change the order of the vectors the cross product changes its sign. Applying these properties, we can obtain a more simple expression of the cross product
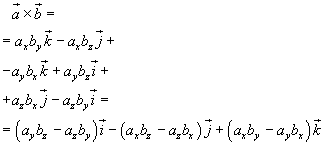
If we know something about the determinants, we can write an even more simple equivalent expression
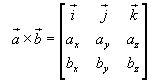
Given the cartesian components of the the vectors a e b and their dot product
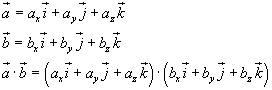
if we apply the distributive law, we'll obtain
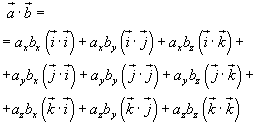
The dot product of a versor by itself is 1 and the dot product of perpendicular vectors is null, so the product is, more simply,
![]()