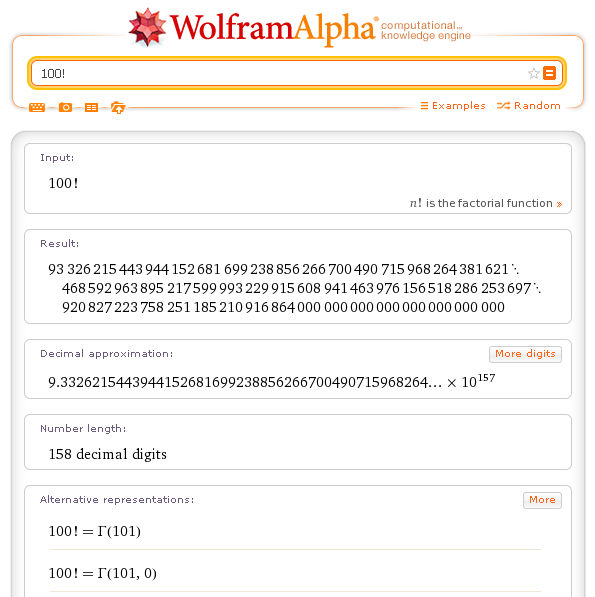
The simplest way to work with Mathematica is to use it as a super calculator, capable of performing exact and approximate numerical calculation to any degree of precision required by the user.
Calculations on integer and rational numbers are always exact and complete, unlike what happens in common pocket calculators that, with rational numbers or with very large integers, inevitably show a limited number of digits.
| Mathematica | result | example |
|---|---|---|
| Prime[n] | computes the n-th prime number | Prime[10] |
| PrimeQ[n] | checks if n is a prime number | PrimeQ[1234567] |
| Divisors[n] | gives the list of the divisors of n | Divisors[1234567] |
| FactorInteger[n] | gives the list of the prime factors of the integer n, together with their exponents | FactorInteger[1234567] |
| Quotient[m,n] | calculates how many times n is contained in m | Quotient[100,7] |
| Mod[m,n] | gives the remainder on division of m by n | Mod[100,7] |
| GCD[i,j,k,m,n,...] | gives the Greatest Common Divisor of the integers within the list | GCD[30,120,45] |
| LCM[i,j,k,m,n,...] | gives the Least Common Multiple of the integers within the list | LCM[30,120,45] |
| Factorial[n] | computes the factorial of n; n! is the same | Factorial[10]; 10! |
| Factorial2[n] | computes the double factorial of n; n!! is the same | Factorial2[10]; 10!! |
| Binomial[n,k] | calculates the binomial coefficient (nk) | Binomial[10,4] |
| Fibonacci[n] | computes the n-th Fibonacci number | Fibonacci[50] |
| BaseForm[n,b] | shows the numbers n given in base b | BaseForm[1024,2] |
Examples

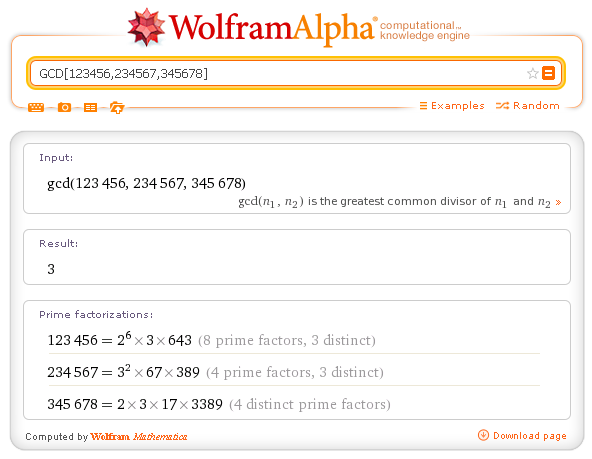
The operator Table allows us to generate lists of objects.
Table requires at least two arguments: a function of one or more variables and one or more lists whose first element is a variable that can be followed or by the last value assumable (the first is the default 1) or by the first and last values assumed. In this way, the variable (for example n which in this case is a simple counter) is incremented by one unit at each step.
Example.

The outcome of the operator Table can be modulated by the operator MatrixForm that formats the output on multiple lines in columns.
Example: the Pythagorean table.
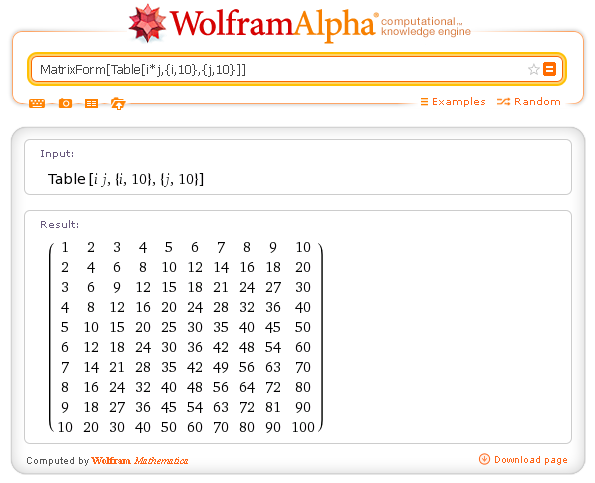
Example: the Pascal's triangle.

In this last example, we used the function If that requires three arguments: a condition, the value if the condition is true, the value if the condition is false.
In general, when we perform operations on whole numbers and fractions, we obtain fractions reduced to lowest terms.
Numerator and Denominator give the numerator or the denominator of a fraction.
Examples
WolframAlpha: Sum of fractions
11 terms of an arithmetic progression with first term 1/2 and common difference 1/3. WolframAlpha: Arithmetic progression
11 terms of a geometric progression with first term 1/2 and common ratio 1/3. WolframAlpha: Geometric progression
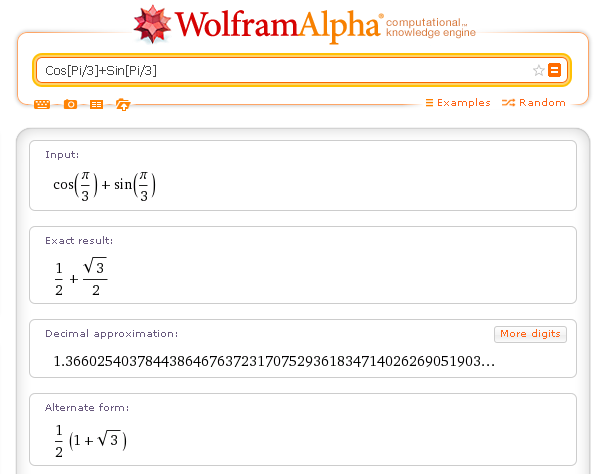
Even in calculations on real and complex numbers Mathematica tries to provide, if possible, mathematically exact results.
For example, if we write
Cos[Pi/3]+Sin[Pi/3]
we get
| Mathematica | result | example |
|---|---|---|
| Pi | the greek pi | Pi/2; Sin[2Pi/3] |
| E | the Euler's number | E^x; Log[Sqrt[E]] |
| GoldenRatio | the number | 1/GoldenRatio |
| Degree | a sexagesimal degree in radians | Sin[60 Degree] |
| I | the imaginary unit | (1+I)^2; Abs[3+4I] |
| Infinity | ∞ | Limit[(x+1)/x,x->Infinity] |
| Mathematica | result | example |
|---|---|---|
| Abs[z] | absolute value | Abs[3+4I] |
| Sqrt[z] | square root | Sqrt[2]; Sqrt[1+I] |
| Exp[z] | natural exponential function (also E^z) | Exp[2]; E^2 |
| Log[z] | natural logarithm | Log[E^2] |
| Log[b,z] | logarithm to the base b | Log[2,8] |
| Sin[z] | circular sine | Sin[Pi/6] |
| Cos[z] | circular cosine | Cos[Pi/6] |
| Tan[z] | circular tangent | Tan[Pi/4] |
| ArcSin[z] | circular arcsine | ArcSin[1/2] |
| ArcCos[z] | circular arccosine | ArcCos[1/2] |
| ArcTan[z] | circular arctangent | ArcTan[Sqrt[3]] |
| Sinh[z] | hyperbolic sine | Sinh[1] |
| Cosh[z] | hyperbolic cosine | Cosh[1] |
| Tanh[z] | hyperbolic tangent | Tanh[1] |
| ArcSinh[z] | hyperbolic arcsine | ArcSinh[1] |
| ArcCosh[z] | hyperbolic arccosine | ArcCosh[1/2] |
| ArcTanh[z] | hyperbolic arctangent | ArcTanh[2] |
Example.
(1+I)^2
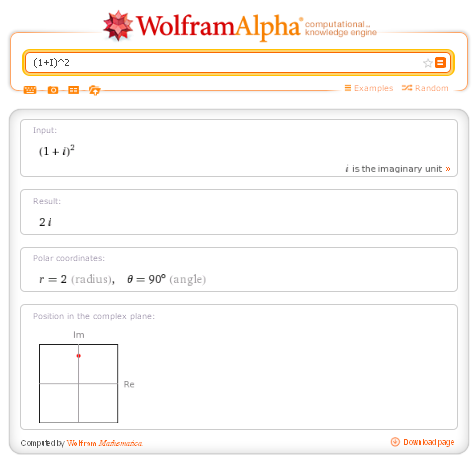
The arguments of the trigonometric functions are always in radians.
If we want the argument in degrees we must multiplicate the argument by the constant Degree.
Other examples.