| Mathematica | result | example |
|---|---|---|
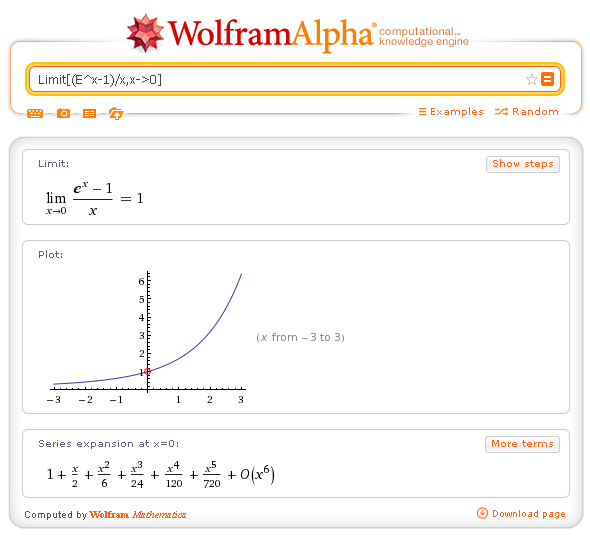
| Limit[f[x],x->x0] | calculate the limit as x→x0 | Limit[(E^x-1)/x,x->0] |
| Limit[f[x],x->Infinity] | calculate the limit as x→∞ | Limit[1/x,x->Infinity] |
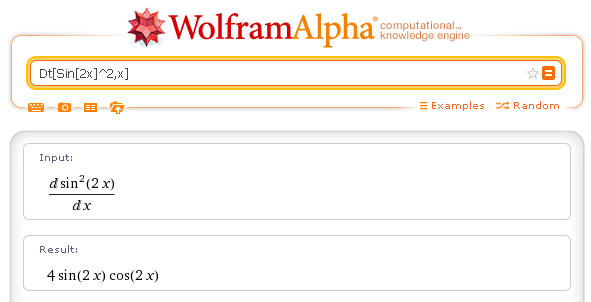
| Dt[f[x],x] | calculates the first derivative of f(x) with respect to x | Dt[Sin[2x]^2,x] |
| Dt[f[x]] | calculates the total differential of f(x) | Dt[Sin[2x]^2] |
| Dt[f[x],{x,n}] | calculates the n-th derivative of f(x) with respect to x | Dt[Sin[2x]^2,{x,2}] |
| D[f[x,y],x] | calculate the partial derivative of f(x,y) with respect to x | D[Sin[x y],x] |
| D[f[x,y],{x,n}] | calculates the n-th partial derivative of f(x,y) with respect to x | D[Sin[x y],{x,2}] |
| Integrate[f[x],x] | calculates the indefinite integral of f(x) with respect to x | Integrate[Log[x],x] |
| Integrate[f[x],{x,xmin,xmax}] | calculates the definite integral of f(x) with respect to x in the range [xmin,xmax] | Integrate[Log[x],{x,1,E}] |
| DSolve[equation,y,x] | solves a differential equation for the function y, with independent variable x | DSolve[y'[x]==y,y,x] |
| Series[f[x],{x,0,n}] | generates n+1 terms of the expansion in MacLaurin power series for f(x) | Series[Exp[x],{x,0,10}] |
| Series[f[x],{x,x0,n}] | generates n+1 terms of a Taylor power series expansion for f(x) about the point x0 | Series[Log[x],{x,1,10}] |
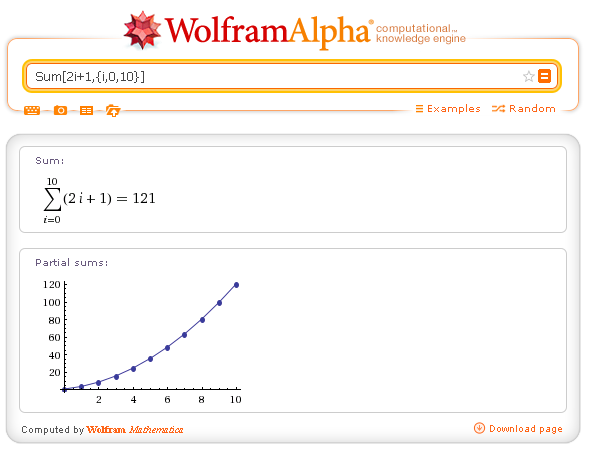
| Sum[f[i],{i,imin,imax}] | calculates the sum of the addends f(i), with i from imin to imax, incrementing i by 1 at each step | Sum[2i+1,{i,0,10}] |
| Sum[f[i],{i,imin,imax,inc}] | calculates the sum of the addends f(i), with i from imin to imax, incrementing i by inc at each step | Sum[2i+1,{i,0,10}] |
Examples with Wolframalpha.
Limit: Limit[(E^x-1)/x,x->0]

Derivative: Dt[Sin[2x]^2,x]
Indefinite integral: Integrate[Log[x],x]
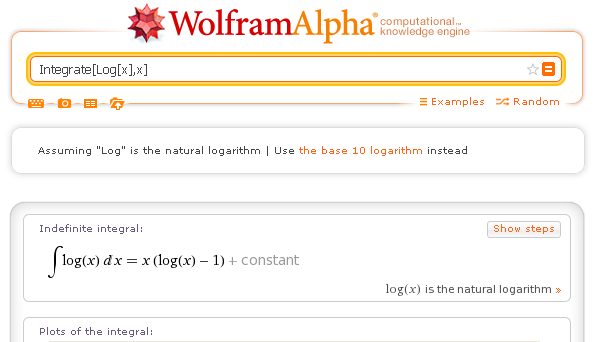
If you click on the button Show steps, you will get the demonstration.
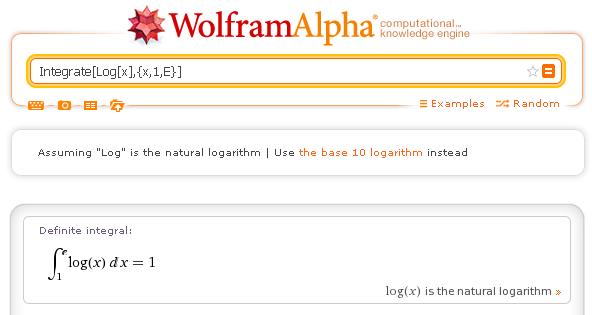
Definite integral: Integrate[Log[x],{x,1,E}]
Differential equazione: DSolve[y'[x]==y,y,x]

If you click on the button Show steps, you will get the demonstration.
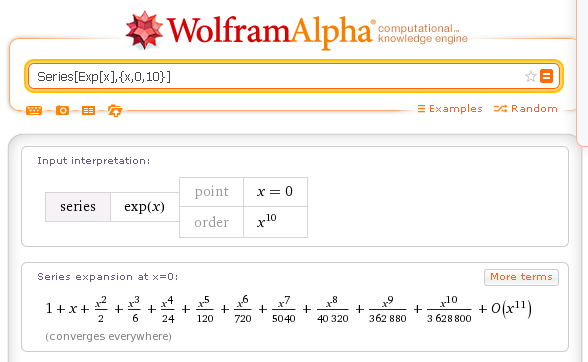
Maclaurin series expansion: Series[Exp[x],{x,0,10}]
The sum of the first 11 odd numbers: Sum[2i+1,{i,0,10}]