In Mathematica, an n-dimensional vector is represented by a list of n elements.
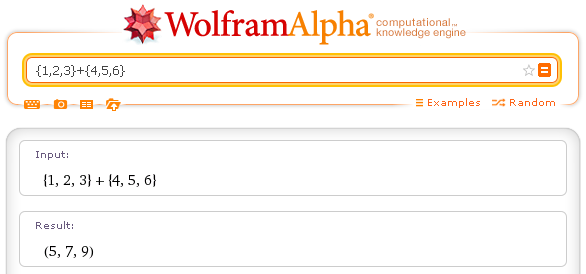
Two vectors of the same size can be added or subtracted to each other.
Example with Wolframalpha.
Sum of three dimensional vectors: {1,2,3}+{4,5,6}

A vector can be multiplied by a scalar.
Example.
Scalar times vector: Sqrt[2]*{Sqrt[2],Sqrt[8],Sqrt[32]}

Vectors of the same size can be scalarly multiplied to obtain a single numerical value. The scalar product is given by
the operator Dot (or simply by the dot .).
Example.
Scalar product of two vectors: Dot[{1,2,3,4},{5,6,7,8}]

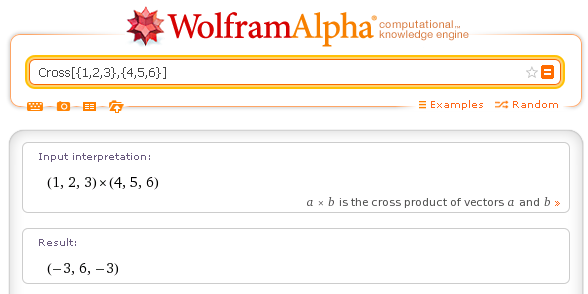
Vectors of the same size can be vectorially multiplied obtaining a vector of size equal to that of the factors and orthogonal to the two factors. Two vectors are orthogonal if their scalar product is 0. The vector (or cross) product is given by the operator Cross.
Example.
Cross product of two vectors: Cross[{1,2,3},{4,5,6}]
Here we limit ourselves to consider square matrices. A square matrix of order n is a table of n rows each consisting of n elements.
In Mathematica a matrix is represented by a list of lists.
Example.
Matrix: {{1,2,3},{2,-1,4},{3,1,5}}

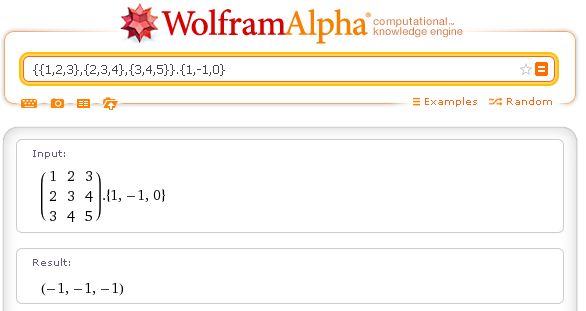
Using Dot (or the simple dot .), you can multiply a square matrix of order n for a vector of order n, obtaining a vector of order n. n
Example.
matrix times vector: {{1,2,3},{2,3,4},{3,4,5}}.{1,-1,0}
Two square matrices of the same order can be added and multiplied together.
Example.
matrix times matrix: {{1,2,3},{2,3,4},{3,4,5}}.{{1,-1,0},{0,1,1},{1,1,0}}
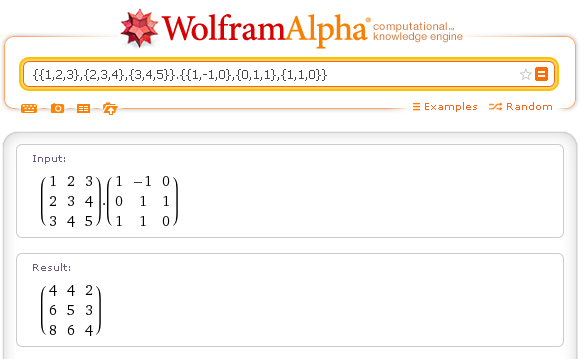
The product is not commutative.
Example.
inverted factors: {{1,-1,0},{0,1,1},{1,1,0}}.{{1,2,3},{2,3,4},{3,4,5}}

You can calculate the determinant of a matrix using the operator Det.
Example.
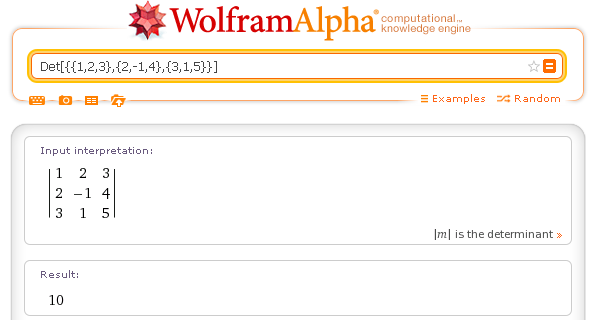
Determinant: Det[{{1,2,3},{2,-1,4},{3,1,5}}]
The operator Inverse produces the inverse matrix of a matrix with non-zero determinant.
Example.
Inverse matrix: Inverse[{{1,2,3},{2,-1,4},{3,1,5}}]

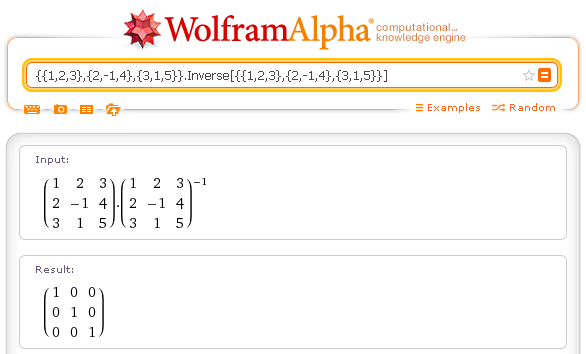
The product of a matrix by its inverse is the neutral matrix.
Example.
matrix times inverse
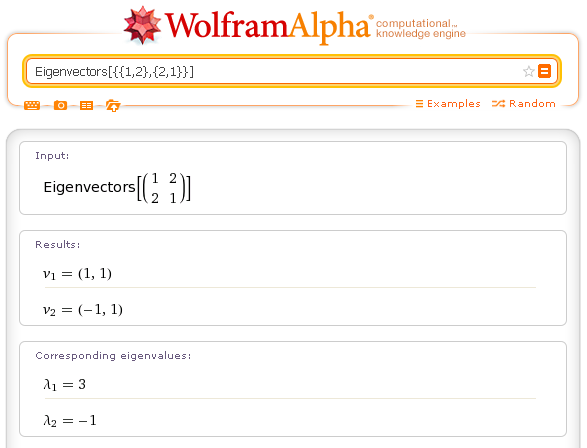
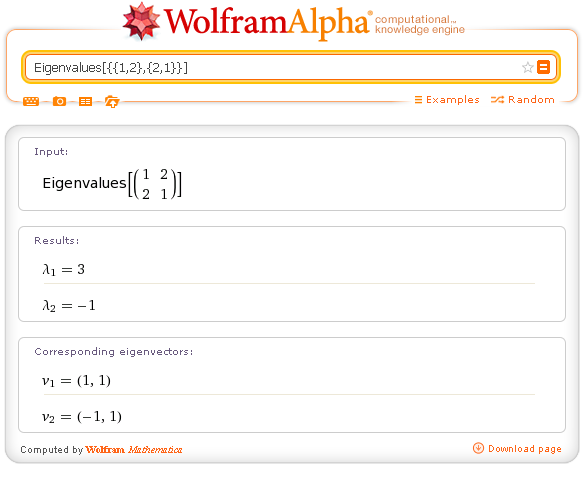
You can get the eigenvalues and the eigenvectors of a square matrix.
Examples.
Eigenvalues[{{1,2},{2,1}}]
Eigenvectors[{{1,2},{2,1}}]