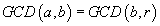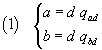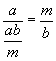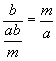The Euclid's algorithm
to calculate the Greatest Common Divisor (GCD) between two natural numbers

(R. Bigoni)

The Euclid's algorithm relies on the following theorem:

Proof

If a is greater than b and isn't multiple of b, said d the GCD(a,b), we have

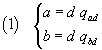
where q_ad and q_bd denote respectively the quotients of the divisions of a by d and of b by d.

If we call q_ab the quotient of the division of a by b and r the remainder of the same division (r < b) we have

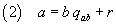
If we now substitute in (2) the second sides of (1) we have

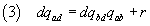
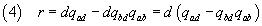
therefore d divides also r.

So

The Least Common Multiple (LCM)

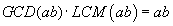
Proof

Let d = GCD(a,b) and m = LCM(a,b).

We have

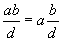• is multiple of a
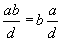• is multiple of b
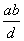• is a common multiple of a e b and, obviously, it is or greater than or equal to m: ;

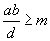Therefore

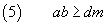
We have also

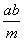• is a divisor of a. Indeed
  
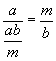
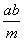• is a divisor of b. Indeed
  
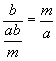
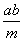• is a common divisor of a and b and, obviously, it is less than or equal to d:

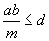
Therefore

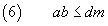
(5) and (6) must hold together, so we have

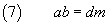
Finally, from (7) we have

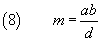
thus

Javascript implementation